資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究C++ 中從先序遍歷恢復樹
假設有一棵二叉樹。我們將對二叉樹的根節點進行先序深度優先搜尋。
在此遍歷中的每個節點，輸出將是 D 個短劃線（其中 D 是該節點的深度），之後我們顯示該節點的值。眾所周知，如果一個節點的深度是 D，則其直接子節點的深度是 D+1，根節點的深度是 0。
我們還需要記住的一件事是，如果一個節點只有一個子節點，則該子節點保證是左子節點。因此，如果給定此遍歷的輸出 S，則恢復樹並返回其根節點。
因此，如果輸入類似於“1-2--3--4-5--6--7”，則輸出將是
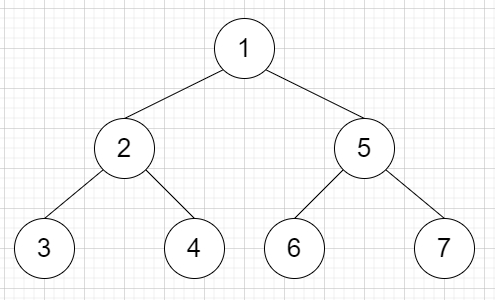
為了解決這個問題，我們將遵循以下步驟：
定義一個棧 st
i := 0，n := S 的大小
lvl := 0，num := 0
當 i < n 時，執行：
對於初始化 lvl := 0，當 S[i] 與 '-' 相同，更新（將 lvl 增加 1），（將 i 增加 1），執行：
不做任何事
num := 0
當 (i < n 且 S[i] 不等於 '-') 時，執行：
num := num * 10 + (S[i] - '0')
（將 i 增加 1）
當 st 的大小 > lvl 時，執行：
從 st 中刪除元素
temp = 建立一個具有 num 值的新樹節點
如果 st 不為空且 st 的頂部元素的左子節點不為空，則：
st 的頂部元素的左子節點 := temp
否則，當 st 不為空時：
st 的頂部元素的右子節點 := temp
將 temp 插入 st
當 st 的大小 > 1 時，執行：
從 st 中刪除元素
返回（如果 st 為空，則返回 NULL，否則返回 st 的頂部元素）
讓我們看看以下實現以更好地理解：
示例
#include <bits/stdc++.h>
using namespace std;
class TreeNode{
public:
int val;
TreeNode *left, *right;
TreeNode(int data){
val = data;
left = NULL;
right = NULL;
}
};
void inord(TreeNode *root){
if(root != NULL){
inord(root->left);
cout << root->val << " ";
inord(root->right);
}
}
class Solution {
public:
TreeNode* recoverFromPreorder(string S) {
stack<TreeNode*> st;
int i = 0;
int n = S.size();
int lvl = 0;
int num = 0;
while (i < n) {
for (lvl = 0; S[i] == '-'; lvl++, i++)
;
num = 0;
while (i < n && S[i] != '-') {
num = num * 10 + (S[i] - '0');
i++;
}
while (st.size() > lvl)
st.pop();
TreeNode* temp = new TreeNode(num);
if (!st.empty() && !st.top()->left) {
st.top()->left = temp;
}
else if (!st.empty()) {
st.top()->right = temp;
}
st.push(temp);
}
while (st.size() > 1)
st.pop();
return st.empty() ? NULL : st.top();
}
};
main(){
Solution ob;
TreeNode *root = ob.recoverFromPreorder("1-2--3--4-5--6--7");
inord(root);
}輸入
"1-2--3--4-5--6--7"
輸出
3 2 4 1 6 5 7
更新於: 2020-06-08
416 次檢視
廣告