資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
Microsoft Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
JavaScript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究用C++構建用於L = {0n1m2(n+m) | m,n ≥ 0}的向下推自動機
我們得到了一種語言“L”，任務是為該語言構建一個下推自動機，這說明2的出現次數將是0和1出現次數的和，並且0和1的出現次數至少為一，也可以使字串為空，並且應該被自動機接受。
什麼是下推自動機？
下推自動機（PDA）是一種以類似於我們為正則文法設計確定性有限自動機 (DFA) 的方式實現上下文無關文法的方法。DFA可以操作有限資料，但PDA可以操作無限資料。我們可以將下推自動機理解為“有限狀態機”和“堆疊”的組合。
下推自動機具有三個組成部分：
一個輸入帶；
一個控制單元；以及
一個無限大小的堆疊。
PDA可以形式化地描述為一個7元組 (Q, Σ, S, δ, q0, I, F)：
Q是有限數量的狀態
Σ是輸入字母表
S是堆疊符號
δ是轉移函式：Q × (Σ υ {ε}) × S × Q × S*
q0是初始狀態 (q0 ∈ Q)
I是初始堆疊頂部符號 (I ∈ S)
F是一組接受狀態 (F ∈ Q)
**讓我們為給定的語言構建一個下推自動機：**
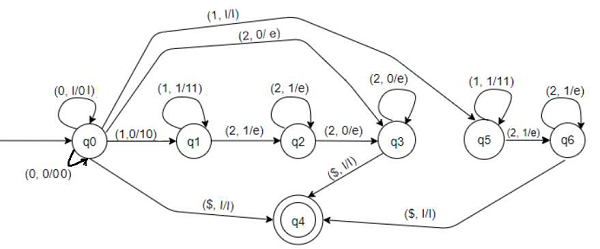
這個PDA可以接受的字串形式為：
0n2n - 02, 0022, 000222 等。0的個數等於2的個數。當m為0時，我們將沒有1。不斷壓入0，一旦遇到第一個2，則彈出0。如果我們到達字串的末尾並且沒有剩餘的0，則接受該字串。
1m2m - 12, 1122, 111222 等。1的個數等於2的個數。當n為0時，我們將沒有0。不斷壓入1，一旦遇到第一個2，則彈出1。如果我們到達字串的末尾並且沒有剩餘的1，則接受該字串。
0n1m2m+n - 0122, 001112, 001112 等。2的個數等於0和1個數之和。不斷壓入0和1。一旦遇到第一個2，則彈出1和0。如果我們到達字串的末尾並且沒有剩餘的0，則接受該字串。
空字串也被接受。001020。
讓我們瞭解一下這個機器
狀態q0的轉移
-(0, I/0I) - 如果堆疊頂部是I且當前輸入符號是0，則將0壓入堆疊頂部並保持在q0。堆疊變為0I…
(0, 0/00) - 如果堆疊頂部是0且當前輸入符號也是0，則將0壓入堆疊頂部並保持在q0。堆疊變為00… 繼續壓入0，直到下一個1或2。
(1, 0/10) - 如果堆疊頂部是0且當前輸入符號是1，則將1壓入堆疊頂部並移動到q1。堆疊變為10…
(1, I/I) - 如果堆疊頂部是I且當前輸入符號是1，則什麼也不做並移動到q5。
(2, 0/ε) - 如果堆疊頂部是0且當前輸入符號是2，則彈出0並移動到q3。
($, I/I) - 如果堆疊頂部是I且沒有輸入，則什麼也不做並移動到q4。對於空字串。
狀態q1的轉移
-(1, 1/11) - 如果堆疊頂部是1且當前輸入符號也是1，則將1壓入堆疊頂部並保持在q1。堆疊變為11… 繼續壓入1，直到下一個2。
(2, 1/ε) - 如果堆疊頂部是1且當前輸入符號是2，則彈出1並移動到q2。
狀態q2的轉移
-(2, 1/ε) - 如果堆疊頂部是1且當前輸入符號是2，則彈出1並保持在q2。
(2, 0/ε) - 如果堆疊頂部是0且當前輸入符號是2，則彈出0並移動到q3。
狀態q3的轉移
-(2, 0/ε) - 如果堆疊頂部是0且當前輸入符號是2，則彈出0並移動到q4。
($, I/I) - 如果堆疊頂部是I且沒有輸入，則什麼也不做並移動到q4。對於空字串。
狀態q5的轉移
-(1, 1/11) - 如果堆疊頂部是1且當前輸入符號也是1，則將1壓入堆疊頂部並保持在q5。堆疊變為11… 繼續壓入1，直到下一個2。
(2, 1/ε) - 如果堆疊頂部是1且當前輸入符號是2，則彈出1並移動到q6。
狀態q6的轉移
-(2, 1/ε) - 如果堆疊頂部是1且當前輸入符號是2，則彈出1並保持在q6。
($, I/I) - 如果堆疊頂部是I且沒有輸入，則什麼也不做並移動到q4。對於空字串。
瀏覽量：302
