構建一個字串的DFA，其中從右側數第二個字元為'a'

確定性有限自動機 (DFA) 是一個 5 元組

M=(Q, Σ, δ,q0,F)

其中，

• Q：稱為狀態的有限集。
• Σ：稱為字母表的有限集。
• δ：Q × Σ → Q 是轉移函式。
• q0 ϵ Q 是起始狀態或初始狀態。
• F：最終狀態或接受狀態。

問題

設計一個有限自動機，其中從右側數第二個字元為'a'。

解決方案

給定字母表 {a,b} 上的字串的語言為 -

L={aa,abaa,abbab,aaabab,………}

示例

輸入 - aaba

輸出 - 未接受

因為從右側數第二個字母不是 a

輸入 - aabbab

輸出 - 接受

直接構建 DFA 比較複雜。

因此，首先嚐試設計非確定性有限自動機 (NFA)，然後將其轉換為確定性有限自動機 (DFA)。

現在構建包含所有字串的語言的 NFA，其中從 RHS 數第 2 個字元為“a”，如下所示 -

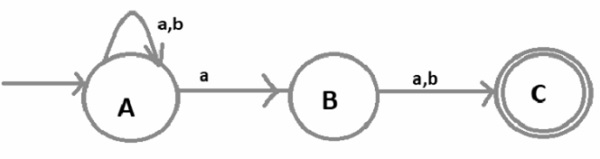
這裡，

• A 是初始狀態。
• B 是中間狀態，並且
• C 是最終狀態。

構建 NFA 轉移表。藉助轉移表，可以很容易地從那裡將 DFA 轉移錶轉換為 DFA 轉移圖。

NFA 轉移表如下所示 -

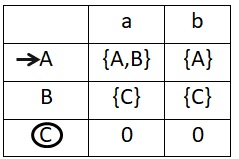
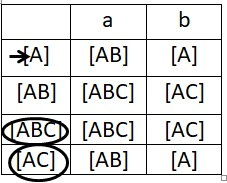
現在將此 NFA 轉移錶轉換為 DFA 轉移表。

我們可以透過在 NFA 的狀態轉移表上使用子集配置來做到這一點。

DFA 轉移表如下所示 -

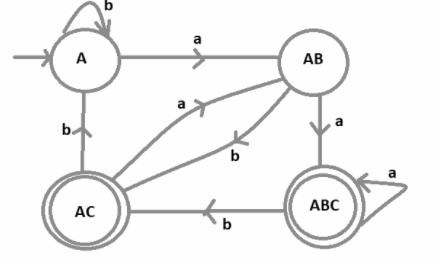
現在，藉助其轉移表，繪製 DFA 比較容易。

在此 DFA 中，有四個不同的狀態 A、AB、ABC 和 AC，其中 ABC 和 AC 是最終狀態，因為 c 是 NFA 中的最終狀態，無論出現 C 的位置，該狀態都成為最終狀態，而 A 是 DFA 的初始狀態。

Bhanu Priya

更新於： 2021 年 6 月 15 日

3K+ 瀏覽量

開啟你的 職業生涯

透過完成課程獲得認證

開始學習