DFA 接受包含“aba”作為子字串的所有字串 w ∈(a,b)* 的 C 程式
問題
設計一個用於語言 L={w1abaw2 | w1,w2 Є(a,b)*} 的 DFA,這意味著 DFA 接受所有包含“aba”作為子字串的字串。
解決方案
語言 L= {aba,aabaa, aabab, babab, ababa, …….} 接受的字串。
步驟 1 - 最小字串(起始字串)的轉換圖 -
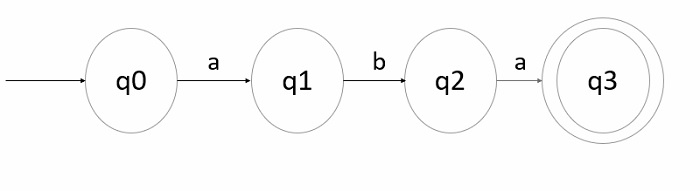
如果 w1 和 w2 為空,則生成的字串為“aba”,因為 w1、w2 ε(a,b)*
q0 是初始狀態,q3 是最終狀態。
步驟 2 - 給定語言的最終 DFA 如下所示 -
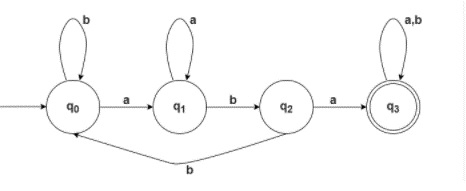
解釋
qo 是初始狀態,q0 在 'a' 上轉到 q1,在 'b' 上轉到 q0,根據 DFA,每個狀態都必須對兩個輸入生成一個轉換。
q1 在 'a' 上轉到 q1,在 'b' 上轉到 q2,我們必須牢記根據給定的語言,我們需要生成一個子字串“aba”。
q2 在 'a' 上轉到 q3,在 'b' 上轉到 q0 狀態。
q3 是最終狀態,在輸入 'a' 和 'b' 上都只轉到 q3。
轉換表
讓我們看看如下所示的轉換表 -
| 當前狀態 | 輸入 a | 輸入 b |
|---|---|---|
| q0 | q1 | q0 |
| q1 | q1 | q2 |
| q2 | q3 | q0 |
| *q3 | q3 | q3 |
示例
以下是構建 DFA 的 C 程式,該 DFA 接受所有包含“aba”作為子字串的字串 w ε(a,b)* -
#include <stdio.h>
#include <string.h>
void checkDFA(char s[] ) {
// storing initial state
int initialState = 0;
//assign initial state to previous state.
int previousState = initialState;
int finalState;
for(int i = 0; i < strlen(s); i++) {
if((previousState == 0 && s[i] == 'a') || (previousState == 1 && s[i] == 'a')) {
finalState = 1;
}
if((previousState == 0 && s[i] == 'b') || (previousState == 2 && s[i] == 'b')) {
finalState = 0;
}
if(previousState == 1 && s[i] == 'b') {
finalState = 2;
}
if((previousState == 2 && s[i] == 'a') || (previousState == 3)) {
finalState = 3;
}
previousState = finalState;
}
if(finalState == 3) {
printf("given string is Accepted");
}
else
{
printf("given string is Not Accepted");
}
}
int main() {
// Given string
char s[40];
printf("implementation of DFA which having a sub string 'aba':
enter a string:");
scanf("%s",s);
checkDFA(s);
return 0;
}輸出
輸出如下所示 -
Run 1: implementation of DFA which having a sub string 'aba': enter a string:aba given string is Accepted. Run 2: implementation of DFA which having a sub string 'aba': enter a string:abba given string is Not Accepted.

廣告

 資料結構
資料結構 網路
網路 關係型資料庫管理系統
關係型資料庫管理系統 作業系統
作業系統 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 程式設計
C 程式設計 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP