廣度優先搜尋是機器學習中統一代價搜尋的一種特殊情況

在本文中，我們將學習廣度優先搜尋是如何成為機器學習中統一代價搜尋的一種特定情況的。無論是誰在執行（人類或人工智慧），他們都必須考慮從改變初始狀態到目標狀態（如果存在）可能產生的所有場景，以及所有可以想象的結果。人工智慧系統也是如此，它們根據所需狀態（如果存在）採用各種搜尋方法。

什麼是廣度優先搜尋？

它是一種人工智慧搜尋方法，它以廣度優先的方式探索樹以找到目標。最常見的方法是廣度優先搜尋演算法（BFS）。BFS 是一種圖遍歷技術，您從源節點開始，並遍歷圖，研究與源節點緊密相關的節點。然後，在 BFS 遍歷中，您必須轉到下一級的鄰居節點。

根據 BFS，您必須以廣度優先的方向探索圖 -

  • 首先水平移動並訪問當前層中的所有節點。
  • 繼續到下一層。

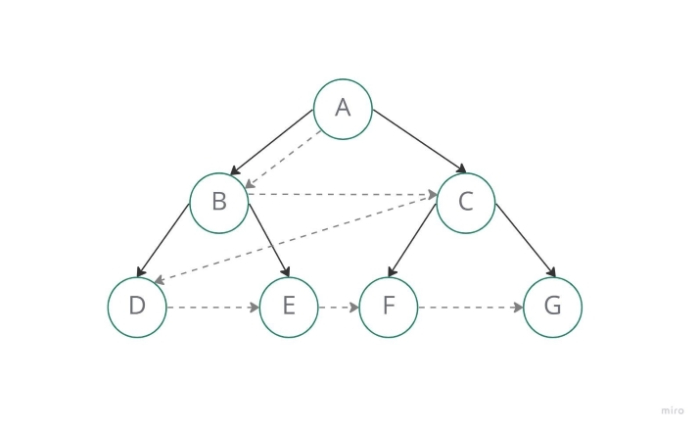
在執行廣度優先搜尋時，使用佇列資料結構來儲存節點並在其標記了所有與其直接連線的相鄰頂點後將其標記為“已訪問”。根據先進先出（FIFO）原則，佇列按新增節點的順序檢視每個節點的鄰居，從第一個放置的節點開始。

優點

  • 只要有解決方案可用，BFS 就會提供它。

  • 如果某個問題有多個解決方案，BFS 將提供步驟最少且成本最低的解決方案。

缺點

  • 由於必須在擴充套件到下一層之前將樹的每一層都儲存在記憶體中，因此需要大量的記憶體。

  • 如果答案位於遠離根節點的位置，則 BFS 需要大量時間。

虛擬碼

Bredth_First_Serach( G, A ) // G is the graph, and A is the source node
Let q be the queue
q.enqueue( A ) // Inserting source node A to the queue
Mark A node as visited.
While ( q is not empty )
B = q.dequeue( ) // Removing that vertex from the queue, which will be
visited by its neighbour
Processing all the neighbours of B
For all neighbours of C of B
C is not visited, q. enqueue( C ) //Stores C in q to visit its neighbour
Mark C a visited

什麼是統一代價搜尋？

當步驟成本不同但必須以最佳方式解決目標狀態時，通常會使用此方法。當這種情況發生時，我們使用統一代價搜尋來識別目標以及路徑，其中包括從根節點到目標節點擴充套件每個節點所產生的總成本。它不會深度或廣度搜索；相反，它尋找具有最低成本的下一個節點。在成本相同的路徑的情況下，讓我們考慮詞典順序。

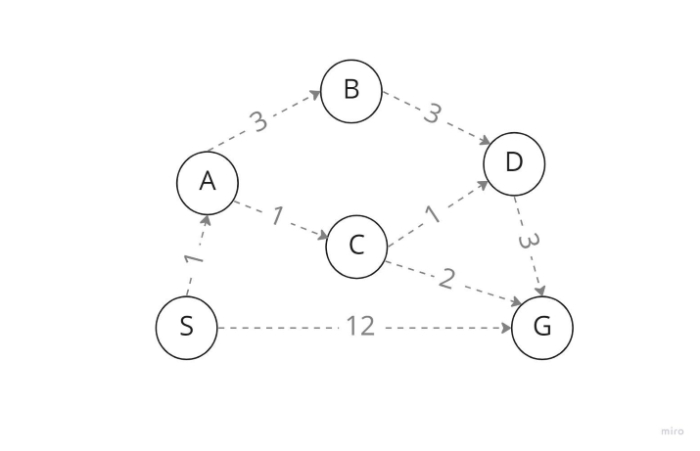
在上圖中，將 S 視為起始節點，將 G 視為目標狀態。我們搜尋要從節點 S 擴充套件的節點，我們的選擇是節點 A 和 G。但是，因為這是統一代價搜尋，所以它擴充套件了具有最低步驟成本的節點，使節點 A 成為後繼節點而不是我們需要的目標節點 G。我們從 A 檢查 B 和 C，A 的子節點。因此，由於節點 C 具有最低的步驟成本，因此它透過節點 C 遍歷。然後，由於節點 D 和 G 是 C 的後繼節點並且具有較低的步驟成本，因此我們也使用 D 進行擴充套件。

最後，透過使用 UFS 演算法，我們獲得了目標狀態 D，因為 D 只有一個子節點 G，這是我們需要的有條件的目標狀態。如果我們走過這條路線，我們的總路徑成本從 S 到 G 只有 6，即使經過多個節點（就步驟成本而言），而不是直接到達 G，其中成本為 12 且 6<<12。但並非每種情況都適合這種情況。

優點

  • 在每個狀態下選擇成本最低的路徑，使統一代價搜尋成為最佳選擇。

缺點

  • 它主要關注路徑成本，而不考慮搜尋過程中涉及多少步驟。因此，此演算法可能會陷入無限迴圈。

虛擬碼

function UCS(Graph, start, target):
   Add the starting node to the opened list. The node has
   has zero distance value from itself
   while True:
      if opened is empty:
         break # No solution found
      selecte_node = remove from opened list, the node with
         the minimun distance value
      if selected_node == target:
         calculate path
         return path
      add selected_node to closed list
      new_nodes = get the children of selected_node
      if the selected node has children:
         for each child in children:
            calculate the distance value of child
            if child not in closed and opened lists:
               child.parent = selected_node
               add the child to opened list
      else if child in opened list:
         if the distance value of child is lower than 
            the corresponding node in opened list:
               child.parent = selected_node
               add the child to opened list

從廣度優先搜尋驅動統一代價搜尋

UCS 透過新增三個更改來增強廣度優先搜尋。

首先，它使用優先順序佇列作為其邊界。它根據 g（從起始節點到邊界節點的路徑成本）對邊界節點進行排序。在選擇節點進行擴充套件時，UCS 從邊界中選擇 g 值最小的節點，即成本最低的節點。

但是，僅僅因為我們將節點新增到邊界並不意味著我們知道到節點狀態的最佳路徑成本。如果我們擴充套件節點 v 並發現從 v 到其鄰居 u 的路徑比 g(w) 成本更低，其中 w 是表示與 u 相同狀態的邊界節點，我們應該從邊界中刪除 w 並用 u 替換它。第二個變化是佇列更新步驟。

第三個是在我們擴充套件節點後執行目標測試，而不是在我們將其放入邊界時執行。如果我們在將節點放入佇列之前對其進行驗證，我們可能會返回到目標的次優路徑。為什麼？因為 UCS 能夠在其執行的後期識別出更好的路徑。

考慮以下廣度優先搜尋返回的次優路徑示例。如果我們在擴充套件 Start 後立即停止搜尋並看到目標節點 Goal 是其鄰居，我們將錯過經過 A 的理想路徑。

結論

用於搜尋的無資訊搜尋技術是一種多功能策略，它結合了無引導搜尋的能力和蠻力。由於它們缺乏有關狀態空間和目標問題的知識，因此此技術的演算法可用於解決各種計算機科學問題。

更新於：2022 年 10 月 28 日

2K+ 次檢視

開啟你的 職業生涯

透過完成課程獲得認證

開始
廣告

© . All rights reserved.