無權圖的應用、優點和缺點

---

圖是如何工作的？

一組相互連線的事物被稱為圖。它們可以代表任何事物，從純粹的數學概念到現實生活中的物體、事件和現象。例如，一個圖可以表示一個具有家族關係的個人列表。類似地，一個城市網路透過道路連線在一起。

通常，我們將網路的元素描述為節點或頂點，而它們之間的連線被稱為邊或弧。

圖1 - 帶有節點和邊的圖的視覺化表示

無權圖：它是什麼？

如果沒有任何邊附加成本或權重，則該圖被稱為無權圖。它們只顯示兩個頂點之間存在關係。

簡單來說，當我們關注兩個節點是否連線或斷開連線時，我們將網路稱為無權圖。我們將具有邊連線的節點稱為彼此相鄰或鄰接。

圖2 - 無權圖

在這篇文章中，我們將探討無權圖的簡單性，其中頂點之間的關係以不包含邊權重的複雜性的方式顯示。無權圖在許多不同領域都有許多應用，包括網站和社交網路。瞭解這種型別的圖的優點和缺點及其在解決問題中的應用。

無權圖：優點

• 由於無權圖考慮了任何兩個節點之間是否存在連線，因此這些概念易於閱讀和理解。

• 無權圖比有權圖消耗更少的儲存空間，因為它們只需要少量記憶體來儲存有關邊是否存在的資料。

• 無權圖易於理解，因為它們描述了連線的存在，並且不需要分析邊權重。

• 可以使用無權圖實現樹形資料結構。

• 包括 DFS 和 BFS 在內的幾種演算法都使用無權圖。

• 有助於最佳地視覺化具有連線但大小不可比的問題。

• 由於不需要儲存或處理邊權重，因此無權圖比有權圖更容易處理。

• 無權圖適用於邊權重無關緊要或未知的問題。

• 當邊權重不重要或不明確時，無權圖是最佳選擇。

• 無權圖比有權圖更易於管理，因為它們不需要儲存或操作邊權重。

無權圖：缺點

• 無權圖無法描述某些關係，包括圖中兩個節點之間的成本或距離。

• 在無權圖的情況下，沒有邊權重。因此，對於需要了解節點之間距離或評估最短路徑的目的而言，它沒有幫助。

• 由於它們無法提供有關節點之間連線的值或強度的詳細資訊，因此無權圖可能比有權圖的資訊量少得多。

無權圖：應用

• 使用無權圖顯示在大小方面彼此之間沒有關係的統計資料。

• 無權圖表示計算過程的流程。

• 可以使用節點和邊來表示影像分割，其中節點表示畫素，邊表示鄰接連線。

• 人工智慧可以使用狀態空間表示來解決問題和做出決策。

• 例如，工作場所中的資料網路表示，例如全球資訊網。

無權圖在即時中的使用

• 可以使用無權圖解決難題。

• 此功能可用於確定兩個人在社交網路平臺上是否相互關聯。

• 它用於具有各種實際應用的哈密頓圖，包括基因組對映，以組合多個小的遺傳資訊片段。

• 可以使用此方法表示電路的示意圖。

• 無權圖用於描述遊戲場景中每個可能的移動。

• 因為它以無權圖的形式表示社交網路中人與人之間的聯絡，所以它被用於社交媒體平臺。

鄰接矩陣

鄰接矩陣是表示無權圖的一種有效方法。該矩陣是一個“n”乘“n”的 1 和 0 陣列，其中“n”是節點的總數。如果與元素 $\mathrm{a_{ij}}$ 關聯的值為 1，則存在連線第 i 個節點和第 j 個節點的邊。如果 $\mathrm{a_{ij} \: = \: 0}$，則確實沒有邊連線這兩個節點。

圖3 - 鄰接矩陣示例

兩個基本假設決定了矩陣表示

• 透過將節點對映到整數，可以為每個節點分配不同的整數編號。在上述情況下，對映為 A 到 1，B 到 2，C 到 3，D 到 4，E 到 5。

• 考慮到可用記憶體有足夠的空間來容納它，可以使用節點總數為 n×n 矩陣分配連續的記憶體。

注意 - 如果這些假設不準確或圖看起來很稀疏，則使用鄰接表。

鄰接表

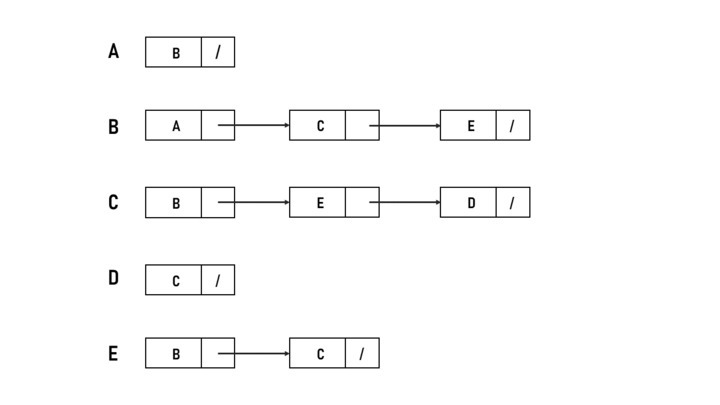
圖4 - 鄰接表示例

您在一個連結串列中跟蹤每個節點的鄰居。這種方法的主要優點是儲存圖資料的記憶體量不需要是連續的。但是，我們確實失去了矩陣表示的“O(1)”訪問複雜性，這是一個寶貴的特性。

無論 i 和 j 的實際值如何，我們都可以以一致的時間量查詢“aij”並獲取有關第 i 個節點和第 j 個節點鄰接的資料。我們可以使用連結串列遍歷整個列表。在最壞的情況下，除搜尋查詢中的第 j 個頂點以外的所有頂點都是第 i 個節點的鄰居。因此，為了確定兩個節點是否沒有連線，我們將檢查連結串列中找到的 [n - 2 ∈ O(n)] 個專案。

結論

本文討論了無權圖的表示。當我們只需要瞭解兩個事物是否透過邊直接連線時，這種型別的圖很有效。