資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
Microsoft Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學基於鳶尾花資料集的決策樹和K均值聚類分析
決策樹和K均值聚類演算法是資料科學和機器學習中常用的技術，用於從大型資料集（如鳶尾花資料集）中發現模式和洞察力。眾所周知，人工智慧廣泛應用於我們的日常生活中，從在移動裝置上閱讀新聞到分析工作中的複雜資料。人工智慧提高了人類工作的速度、準確性和效率。人工智慧的發展使我們能夠完成以前被認為不可能的事情。
在這篇文章中，我們將學習決策樹演算法和K均值聚類演算法，以及如何在鳶尾花資料集上應用它們。
鳶尾花資料集
費雪的鳶尾花資料集是一個多元資料集，由英國統計學家和生物學家羅納德·費雪在他1936年的著作《在分類問題中使用多種測量》中作為線性判別分析的例子而聞名。費雪的工作發表在該期刊上。埃德加·安德森收集了這些資料，以研究三種密切相關的鳶尾花物種的花朵之間存在的形態差異。在加斯佩半島，這三個物種中的兩個物種是“在同一天，同一個人使用相同的測量裝置，從同一個牧場收集的”。
該資料集包含從三個鳶尾花物種（山鳶尾、維吉尼亞鳶尾和變色鳶尾）中收集的50個樣本。對每個樣本都測量了萼片和花瓣的長度和寬度（以釐米為單位）。這是測量的四個特徵中的兩個。
決策樹
決策樹是一種非引數的監督學習方法，常用於分類和迴歸應用。它具有類似樹的分層結構，由根節點、分支、內部節點和葉節點組成。
K均值聚類
K均值聚類是一種向量量化技術，起源於訊號處理領域。其目標是將n個觀測值分成k個聚類，使得每個觀測值都屬於具有最近均值（聚類中心或聚類質心）的聚類，該均值充當聚類的原型。這導致資料空間被劃分為Voronoi單元。雖然幾何中位數是唯一可以最小化歐幾里得距離的，但均值是針對平方誤差最佳化的。例如，可以使用k-medians和k-medoids找到改進的歐幾里得解。
在鳶尾花資料集上應用決策樹和K均值聚類演算法
示例
import pandas as pdd from sklearn import datasets import numpy as npp import sklearn.metrics as smm import matplotlib.patches as mpatchess from sklearn.cluster import KMeans import matplotlib.pyplot as pltt from sklearn.metrics import accuracy_score %matplotlib inline iris = datasets.load_iris() print(iris.target_names) print(iris.target) x1 = pdd.DataFrame(iris.data, columns=['Sepal Length', 'Sepal Width', 'Petal Length', 'Petal Width']) y1 = pdd.DataFrame(iris.target, columns=['Target']) x1.head()
輸出
['setosa' 'versicolor' 'virginica']
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
Sepal Length Sepal Width Petal Length Petal Width
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2
3 4.6 3.1 1.5 0.2
4 5.0 3.6 1.4 0.2
列印目標變數y的前5行：
y1.head()
輸出
Target 0 0 1 0 2 0 3 0 4 0
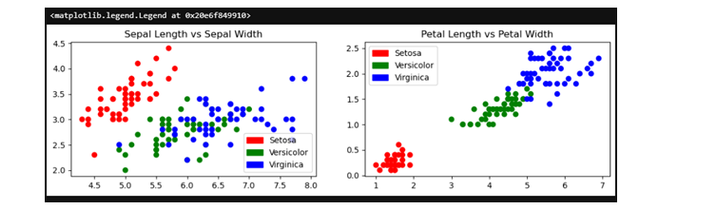
下一步，繪製資料集圖，顯示資料集變數之間的差異：
pltt.figure(figsize=(12,3))
colors = npp.array(['red', 'green', 'blue'])
iris_targets_legend = npp.array(iris.target_names)
red_patch = mpatchess.Patch(color='red', label='Setosa')
green_patch = mpatchess.Patch(color='green', label='Versicolor')
blue_patch = mpatchess.Patch(color='blue', label='Virginica')
pltt.subplot(1, 2, 1)
pltt.scatter(x1['Sepal Length'], x1['Sepal Width'], c=colors[y1['Target']])
pltt.title('Sepal Length vs Sepal Width')
pltt.legend(handles=[red_patch, green_patch, blue_patch])
pltt.subplot(1,2,2)
pltt.scatter(x1['Petal Length'], x1['Petal Width'], c= colors[y1['Target']])
pltt.title('Petal Length vs Petal Width')
pltt.legend(handles=[red_patch, green_patch, blue_patch])
輸出
下一步我們將定義聚類。
iris_k_mean_model = KMeans(n_clusters=3) iris_k_mean_model.fit(x1) print(iris_k_mean_model.labels_)
輸出
KMeans(n_clusters=3) [[5.9016129 2.7483871 4.39354839 1.43387097] [5.006 3.428 1.462 0.246 ] [6.85 3.07368421 5.74210526 2.07105263]]
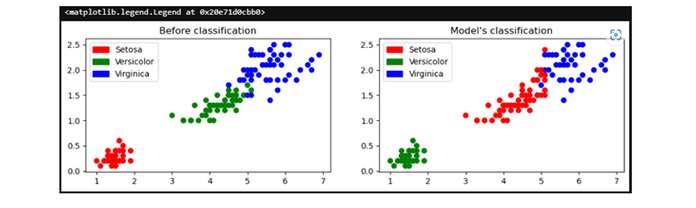
現在，我們將繪製分類前後的圖形：
pltt.figure(figsize=(12,3))
colors = npp.array(['red', 'green', 'blue'])
predictedY = npp.choose(iris_k_mean_model.labels_, [1, 0, 2]).astype(npp.int64)
pltt.subplot(1, 2, 1)
pltt.scatter(x1['Petal Length'], x1['Petal Width'], c=colors[y1['Target']])
pltt.title('Before classification')
pltt.legend(handles=[red_patch, green_patch, blue_patch])
pltt.subplot(1, 2, 2)
pltt.scatter(x1['Petal Length'], x1['Petal Width'], c=colors[predictedY])
pltt.title("Model's classification")
pltt.legend(handles=[red_patch, green_patch, blue_patch])
輸出
下一步，我們將列印模型的準確性：
smm.accuracy_score(predictedY, y1['Target'])
輸出
0.24
下一步，我們將測試模型並列印測試資料集和訓練資料集的準確性：
from sklearn.metrics import accuracy_score
X = iris.data
# Extracting Target / Class Labels
y = iris.target
# Import Library for splitting data
from sklearn.model_selection import train_test_split
# Creating Train and Test datasets
X_train, X_test, y_train, y_test = train_test_split(X,y, random_state = 50, test_size = 0.25)
# Creating Decision Tree Classifier
from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier()
clf.fit(X_train,y_train)
# Predict Accuracy Score
y_pred = clf.predict(X_test)
print("Train data accuracy:",accuracy_score(y_true = y_train, y_pred=clf.predict(X_train)))
print("Test data accuracy:",accuracy_score(y_true = y_test, y_pred=y_pred))
輸出
Train data accuracy: 1.0 Test data accuracy: 0.9473684210526315
結論
總之，鳶尾花資料集是一個常用的機器學習資料集，常用於測試不同的演算法。在這裡，我們使用了流行的決策樹演算法和K均值聚類演算法來分析資料。
透過使用這些方法，我們可以更好地瞭解資料的結構，並利用該結構進行預測和對資料進行分組。
瀏覽量：572
