安培環路定律及其應用

---

介紹

安培定律為電動力學的發展樹立了里程碑。1920 年，漢斯·奧斯特用指南針和載流導線進行了一次經典實驗。他觀察到，如果導線中沒有電流，則指南針始終指向北極。然而，在導線中有電流的情況下，指標會向某個方向偏轉。他發現偏轉方向與圓相切，即磁場方向（圖 1）。

圖 1：載流導線周圍的磁場方向

這表明載流導線在其周圍產生磁場。原則上，我們總是可以使用畢奧-薩伐爾定律來估計載流導線產生的磁場。為了估計任何電流分佈產生的淨磁場，我們首先寫出微分磁場 (dB) ⃗，然後將其在整個分佈上求和。但是，如果我們的電流分佈存在對稱性呢？我們能否簡化計算？答案是肯定的。安培定律幫助我們計算磁場。

安德烈-瑪麗·安培是誰？

安德烈-瑪麗·安培出生於 1775 年，是一位法國物理學家和數學家。他是一位神童，12 歲就開始學習數學。奧斯特發現電流產生磁場，這吸引了他對該領域的興趣。他繼承了奧斯特的工作，並證明了載流導線相互排斥或吸引。這種排斥或吸引取決於導線中電流的方向。他因其著名的成果“安培定律”而聞名。為了紀念他，電流的 SI 單位以他的名字命名。

安培環路定律的表述

安培定律可以這樣表述：“穿過任何閉合迴路的磁場力的線積分與穿過該回路的電流成正比。”

如果有多個電流穿過迴路，我們將取回路包圍的電流的數值和。用於計算的迴路稱為“安培迴路”或“安培線圈”。

安培環路定律的另一種形式

假設存在一個閉合路徑 C，並且穿過它的淨電流為 $\mathrm{i_{enc}}$，則

$$\mathrm{\int \overrightarrow{B}.\overrightarrow{dl}=\mu_0i_{enc}}$$

讓我們分析這個方程式的每一項。

$\mathrm{\overrightarrow{B}}$ 的線積分 - 我們可以將回路分成小的向量元素 $\mathrm{\overrightarrow{dl}}$。然後

$$\mathrm{\overrightarrow{B}.\overrightarrow{dl}=Bdl\:cos\theta}$$

因此，它是線元素和磁場切向部分（Bcosθ）的乘積。迴路。

淨電流 $\mathrm{i_{enc}}$ - 我們需要考慮僅穿過迴路的電流元素的代數和。

從圖中，只有 $\mathrm{i_{enc}=i_1+i_2}$

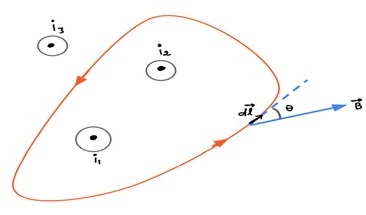
積分方向 - 可以使用右手定則計算積分方向。如果我們彎曲右手，使手指指向積分方向，則伸出的拇指將指向電流的正方向。

安培環路定律的不一致性

讓我們將安培定律應用於下圖所示的情況。我們有一個電容器，傳導（常規）電流用 $\mathrm{i_c}$ 表示。根據安培定律，路徑周圍的積分 $\mathrm{\overrightarrow{B}.\overrightarrow{dl}}$ 應該等於 $\mathrm{μ_0 i_{enc}}$

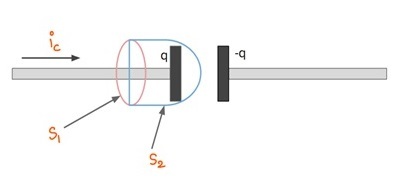
這裡我們取兩個表面。對於表面 $\mathrm{S_1:i_{enc}=i_c}$

對於向右凸出的表面 $\mathrm{S_2}$：$\mathrm{i_{enc} = 0}$，因為電容器間隙之間不存在電流。

這裡 $\mathrm{\overrightarrow{B}.\overrightarrow{dl}}$ 為零，而 $\mathrm{i_c}$ 同時為同一路徑，這與矛盾。

修正的安培環路定律或安培-麥克斯韋環路定律

麥克斯韋透過引入一個稱為“位移電流”的新項來修改安培定律，以消除這種歧義。它被定義為

$$\mathrm{i_d=\epsilon_0\:\frac{d\Phi_E}{dt}}$$

其中 $\mathrm{\Phi_E}$ 是透過表面的電通量，由 $\mathrm{\Phi_E=\int \overrightarrow{E}.\overrightarrow{dA}}$ 給出。

因此，安培定律或安培-麥克斯韋定律的修正形式為 -

$$\mathrm{\int (\overrightarrow{B}).(\overrightarrow{dl})=\mu_0(i_c+i_d)=\mu_0i_c+\mu_0 \epsilon_0 \frac{d\Phi_E}{dt}}$$

現在我們可以使用安培-麥克斯韋定律來解決電容器情況下出現的問題。

如果我們將此定律應用於表面 $\mathrm{S_1:i_{enc}=i_c}$，則與往常一樣

但是對於向右凸出的表面 $\mathrm{S_2}$：$\mathrm{i_{enc} = 0}$，但 $\mathrm{i_d= \epsilon_0 \frac{d\Phi_E}{dt}}$，因為電容器間隙之間的電場將是可變的。

因此，如果迴路內部存在時變場，我們必須使用安培-麥克斯韋定律來解決問題。

安培環路定律的應用

我們可以將安培定律用於電流分佈對稱的各種問題。

讓我們考慮一根半徑為 R 的直導線，它承載電流 i。讓我們應用安培定律來估計該導線在距離 r 處的磁場。(r>>R)

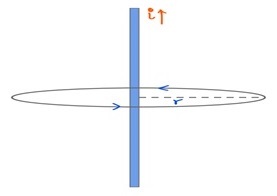
我們可以看到導線具有圓柱對稱性。使用右手定則，我們可以計算 B 的方向。它出現在安培迴路的每個點的切線上，線元素dl與安培迴路平行。這意味著 $\mathrm{\overrightarrow{B}}$ 和 $\mathrm{\overrightarrow{dl}}$彼此平行。

這意味著

$$\mathrm{\overrightarrow{B}.\overrightarrow{dl}=Bdl\:cos\theta = B\:dl\:cos\:0^{\circ}=Bdl}$$

安培定律

$$\mathrm{\int\overrightarrow{B}.\overrightarrow{dl}=\oint B.dl=B\:\oint\:dl=B.2\Pi r = \mu_0 I}$$

因此

$$\mathrm{B =\frac{\mu_0 i}{2\pi r}}$$

這是一個眾所周知的結果，也可以使用畢奧-薩伐爾定律進行驗證。

解題示例

示例 1：求表面 1 和 2 中 $\mathrm{\overrightarrow{B}.\overrightarrow{dl}}$ 的值。

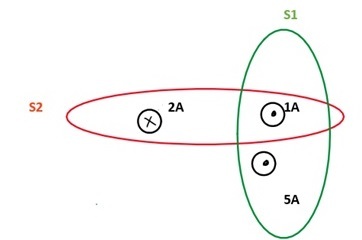
答：我們可以從圖中看到 S1 包含兩個電流 1A 和 $\mathrm{5A.\overrightarrow{B}.\overrightarrow{dl} =6}$ S2 也包含兩個電流，但其中一個方向相反。$\mathrm{\overrightarrow{B}.\overrightarrow{dl}=5-2=3}$

示例 2：一根半徑 R=2cm 的長直導線承載 10A 的電流。求其 8cm 處的磁場？

我們已經推匯出直導線磁場的方程式。我們可以在此處直接使用它。

$$\mathrm{B =\frac{\mu_0 i}{2\Pi r}=\frac{4\Pi\times 10^7\times10}{2\Pi\times 8 \times10^{−2}}=\frac{20\times 10^{−5}}{8}=2.5\times 10^{−5}\:Tesla}$$

結論

我們可以使用安培定律簡化對電流分佈產生的磁場的估計。但只有在系統存在某種對稱性時才能使用它。如果迴路內部存在某些時變電場源，則安培定律無法給出任何合理的結果。麥克斯韋針對此類情況修改了該定律，並引入了位移電流的概念。這可以用電容器的情況來證明。我們可以使用安培定律來估計載流直導線產生的磁場，結果表明它與我們計算磁場的距離成反比。

常見問題

Q1. 寫出除載流導線之外的磁場源？

答：變化的電場也可以產生磁場

Q2. 安培定律在迴路中是否適用於所有型別的電流？

答：否，這些僅適用於穩恆電流。

Q3. 我們可以從安培定律推匯出畢奧-薩伐爾定律嗎？

答：是的，它們可以相互推導。

Q4. 靜電學中相當於安培定律的是什麼？

答：高斯定律相當於安培定律。

Q5. 安培-麥克斯韋定律的結論是什麼？

答：安培-麥克斯韋定律告訴我們，磁場可以透過載流導線以及變化的電場產生。