資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究數字連線遊戲？
數字連線是一種邏輯謎題，涉及在網格中找到連線數字的路徑。
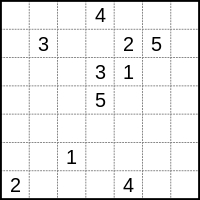
一個簡單的數字連線謎題示例 數字連線謎題的解答
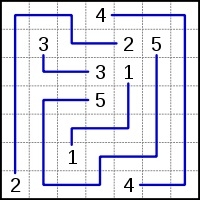
規則 − 玩家必須使用單一的連續線（或路徑）將網格上所有匹配的數字配對。線條不能分叉或交叉，數字必須位於每條線的末端（即，不能位於中間）。只有當謎題有唯一的解且網格中的所有單元格都被填充時，才認為該謎題設計良好，儘管一些數字連線設計者沒有規定這一點。
遊戲 − 考慮一個 n × n 的方格陣列。一些方格是空的，一些是實心的，一些非實心的方格被標記為整數 1、2、3、… 每個整數在棋盤上佔據兩個不同的方格。玩家的任務是使用僅水平和垂直移動的簡單路徑連線棋盤上每個整數的兩個出現位置。不允許兩條不同的路徑相互交叉。任何路徑都不能包含任何實心方格（實心方格被禁止出現在任何路徑上）。最後，所有非實心方格都必須被路徑填充。
演算法 − 要準備一個給定棋盤大小 n × n 的有效隨機謎題，我們首先在棋盤上生成隨機的簡單且互不交叉的路徑。如果一些孤立的方格位於所有生成的路徑之外，則將這些孤立的方格標記為實心（禁止）。然後，我們提供路徑的端點和實心方格的列表作為謎題。
因此，我們首先生成一個解，然後從解中推匯出謎題。路徑和實心方格對 n × n 棋盤進行分割槽。我們使用聯合查詢資料結構來生成此分割槽。該資料結構處理棋盤上 n^2 個方格集合的子集。
解釋
在棋盤上隨機定位方格 (i, j) 和 (k, l)，條件是：(a) (i, j) 和 (k, l) 彼此相鄰，並且 (b) (i, j) 和 (k, l) 均不屬於迄今為止生成的任何路徑。如果在整個棋盤上找不到這樣的方格對，則返回失敗 /* 在這裡，(i, j) 和 (k, l) 是要構造的新路徑上的前兩個方格。*
將包含 (i, j) 和 (k, l) 的兩個聯合查詢樹合併。
重複執行，只要當前路徑可以擴充套件：將 (i, j) 重新命名為 (k, l)。定位 (i, j) 的隨機相鄰方格 (k, l)，條件是：(a) (k, l) 不屬於迄今為止生成的任何路徑（包括當前路徑）(b) (k, l) 在部分構造的當前路徑上唯一的鄰居是 (i, j)。
如果找不到這樣的鄰居 (k, l)，則路徑無法進一步擴充套件，因此退出迴圈
否則，將 (i, j) 和 (k, l) 所屬的兩個聯合查詢樹合併。
設定新路徑開頭和結尾處的兩個方格的端點標誌。
返回成功
輸入
| || || || || || || 4 | | || || || || || 3 || | | || || 2 || 2 || || || 3 | | || || || || X || || 1 | | || || 6 || || || 7 || 7 | | 5 || 4 || || X || || X || 1 | | || 5 || || 6 || || || |
輸出
上述表格的解決方案
| 4 || 4 || 4 || 4 || 4 || 4 || 4 | | 4 || 1 || 1 || 1 || 1 || 3 || 3 | | 4 || 1 || 2 || 2 || 1 || 1 || 3 | | 4 || 1 || 1 || 1 || X || 1 || 1 | | 4 || 4 || 6 || 1 || 1 || 7 || 7 | | 5 || 4 || 6 || X || 1 || X || 1 | | 5 || 5 || 6 || 6 || 1 || 1 || 1 |
示例
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
struct _node {
struct _node *parent;
int rank;
int path_number;
int endpoint;
};
typedef struct _node node;
/* Name: initboard()
Input: 2D-array of pointers, size of array row/column
Output: --void--
Description: Takes a table of pointers and initializes it. */
void initboard(node ***arr, int n) {
int i, j;
for (i=0;i<n;i++){
for (j=0;j<n;j++){
node *np;
np = (node *)malloc(sizeof(node));
np->rank = 0;
np->parent = NULL;
np->path_number = 0;
np->endpoint = 0;
arr[i][j] = np;
}
}
}
/*Input:a node Output:the set pointer of the set the node belongs to
描述 − 獲取一個節點並返回集合指標。 */
node *findset(node *n) {
if (n->parent != NULL)
n = n->parent;
return n;
}
void setunion(node *x, node *y) {
x = findset(x);
y = findset(y);
if (x->rank > y->rank)
y->parent = x;
else {
x->parent = y;
if(x->rank == y->rank)
y->rank++;
}
}
int neighbour(int n, node ***arr) {
int i1, i2, j1, j2, ct = 0, flag = 0, a, b,k2;
int k = rand()%(n*n);
while (ct < (n*n)) {
k %= (n*n);
i1 = k/n;
j1 = k%n;
if (arr[i1][j1]->path_number==0) {
int kk = rand()%4;
int cc = 0;
switch (kk) {
case 0: i2= i1-1;
j2= j1-0;
if(i2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 1: i2= i1-0;
j2= j1-1;
if(j2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 2: i2= i1+1;
j2= j1-0;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 3: i2= i1-0;
j2= j1+1;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 4: if(cc==4)
break;
i2= i1-1;
j2= j1-0;
if(i2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 5: if(cc==4)
break;
i2= i1-0;
j2= j1-1;
if(j2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 6: if(cc==4)
break;
i2= i1+1;
j2= j1-0;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
case 7: if(cc==4)
break;
i2= i1-0;
j2= j1+1;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
flag=1;
break;
}
}
cc++;
}
}
if(flag==1)
break;
ct++;
k++;
}
if(ct<n*n) {
k2= (i2*n)+j2;
return k*(n*n)+k2;
} else {
return -1;
}
}
int checkneigh(int k1, int k2, int n, node ***arr) {
int i= k2/n;
int j= k2%n;
int ii= k1/n;
int jj= k1%n;
int ct=0;
if(i>0 && findset(arr[i-1][j])==findset(arr[ii][jj]))
ct++;
if(i<n-1 && findset(arr[i+1][j])==findset(arr[ii][jj]))
ct++;
if(j>0 && findset(arr[i][j-1])==findset(arr[ii][jj]))
ct++;
if(j<n-1 && findset(arr[i][j+1])==findset(arr[ii][jj]))
ct++;
if(ct>1)
return 0;
else
return 1;
}
int valid_next(int k, int n, node ***arr) {
int i1, i2, j1, j2, a, b, kk, stat,ct=0;
int flag=0;
i1= k/n;
j1= k%n;
kk= rand()%4;
switch(kk) {
case 0: i2= i1-1;
j2= j1-0;
if(i2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 1: i2= i1-0;
j2= j1-1;
if(j2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d
",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 2: i2= i1+1;
j2= j1-0;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d
",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 3: i2= i1-0;
j2= j1+1;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d
",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 4: if(ct==4)
break;
i2= i1-1;
j2= j1-0;
if(i2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d
",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 5: if(ct==4)
break;
i2= i1-0;
j2= j1-1;
if(j2>=0 && i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d
",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 6: if(ct==4)
break;
i2= i1+1;
j2= j1-0;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d
",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
case 7: if(ct==4)
break;
i2= i1-0;
j2= j1+1;
if(i2<n && j2<n) {
if(arr[i2][j2]->path_number==0) {
stat= checkneigh(k, (n*i2 + j2),n,arr);
//printf("%d
",stat);
if(stat) {
flag=1;
break;
}
}
}
ct++;
}
//printf("flag- %d
",flag);
if(flag==0)
return -1;
if(flag) {
//printf("value sent- %d
", i2*n + j2);
return (i2*n)+j2;
}
}
int addpath(node ***arr, int n, int ptno) {
int a,b,k1,k2;
int i1,j1,i2,j2;
k2= neighbour( n, arr);
if(k2==-1) //no valid pair found to start with
return 0;
k1= k2/(n*n);
k2= k2%(n*n);
//printf("%d %d
",k1,k2);
i1= k1/n;
j1= k1%n;
i2= k2/n;
j2= k2%n;
arr[i1][j1]->endpoint= 1;
arr[i2][j2]->path_number= ptno;
arr[i1][j1]->path_number= ptno;
node *n1, *n2;
n1= arr[i1][j1];
n2= arr[i2][j2];
n1= findset(n1);
n2= findset(n2);
setunion(n1, n2);
while(1) {
i1= i2;
j1= j2;
k1= (i1*n)+j1;
k2= valid_next(k1,n,arr);
if(k2==-1) {
arr[i1][j1]->endpoint= 1;
break;
}
i2=k2/n;
j2=k2%n;
arr[i2][j2]->path_number= ptno;
node *n1, *n2;
n1= arr[i1][j1];
n2= arr[i2][j2];
n1= findset(n1);
n2= findset(n2);
setunion(n1,n2);
}
return 1;
}
void printtable(node ***arr, int n) {
int i,j;
printf("Table to be solved:
");
for(i=0;i<n;i++) {
for(j=0;j<n;j++) {
if(arr[i][j]->endpoint ==1){
if(arr[i][j]->path_number/10==0)
printf("| %d |",arr[i][j]->path_number);
else
printf("| %d|",arr[i][j]->path_number);
} else if(arr[i][j]->path_number==0)
printf("| X |");
else
printf("| |");
}
printf("
");
}
printf("
The solution to the above table:
");
for(i=0;i<n;i++) {
for(j=0;j<n;j++) {
if(arr[i][j]->path_number != 0){
if(arr[i][j]->path_number/10==0)
printf("| %d |",arr[i][j]->path_number);
else
printf("| %d|",arr[i][j]->path_number);
} else
printf("| X |");
}
printf("
");
}
}
int main(void) {
srand((unsigned int) time (NULL));
int i, j;
int ct = 1;
int n = 7;
node*** pointers= (node ***)malloc(n*sizeof(node **));
for (i=0; i<n; i++)
pointers[i] = (node **)malloc(n*sizeof(node *));
initboard(pointers, n);
while(1) {
i = addpath(pointers, n, ct);
if (i==0) {
break;
} else {
ct++;
}
}
printtable(pointers,n);
return 0;
}
更新於： 2020年7月2日
572 次檢視
廣告