資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚學
法律學拉格朗日插值
對於在離散給定資料點範圍之內構造新的資料點，使用插值技術。拉格朗日插值技術就是其中之一。當給定資料點分佈不均勻時，我們可以用此插值法找出解決方案。對於拉格朗日插值法，我們必須遵循此方程式。
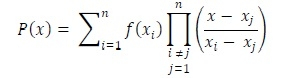
輸入和輸出
Input:
List of x and f(x) values. find f(3.25)
x: {0,1,2,3,4,5,6}
f(x): {0,1,8,27,64,125,216}
Output:
Result after Lagrange interpolation f(3.25) = 34.3281演算法
largrangeInterpolation(x: array, fx: array, x1)
輸入 − x 陣列和 fx 陣列，用於獲取以前已知的資料，以及點 x1。
輸出：f(x1) 的值。
Begin res := 0 and tempSum := 0 for i := 1 to n, do tempProd := 1 for j := 1 to n, do if i ≠ j, then tempProf := tempProd * (x1 – x[j])/(x[i] – x[j]) done tempPord := tempProd * fx[i] res := res + tempProd done return res End
示例
#include<iostream>
#define N 6
using namespace std;
double lagrange(double x[], double fx[], double x1) {
double res = 0, tempSum = 0;
for(int i = 1; i<=N; i++) {
double tempProd = 1; //for each iteration initialize temp product
for(int j = 1; j<=N; j++) {
if(i != j) { //if i = j, then denominator will be 0
tempProd *= (x1 - x[j])/(x[i] - x[j]); //multiply each term using formula
}
}
tempProd *= fx[i]; //multiply f(xi)
res += tempProd;
}
return res;
}
main() {
double x[N+1] = {0,1,2,3,4,5,6};
double y[N+1] = {0,1,8,27,64,125,216};
double x1 = 3.25;
cout << "Result after lagrange interpolation f("<<x1<<") = " << lagrange(x, y, x1);
}輸出
Result after lagrange interpolation f(3.25) = 34.3281
更新於：2020 年 6 月 17 日
988 次瀏覽
廣告