資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究星三角啟動器的工作原理
星三角啟動器的電路圖和工作原理
該圖顯示了三相非同步電動機與星三角啟動器的連線圖。星三角啟動器是一種非常常見的啟動器，廣泛用於啟動鼠籠式非同步電動機。它用於啟動設計為在三角形連線定子繞組上正常執行的鼠籠式非同步電動機。
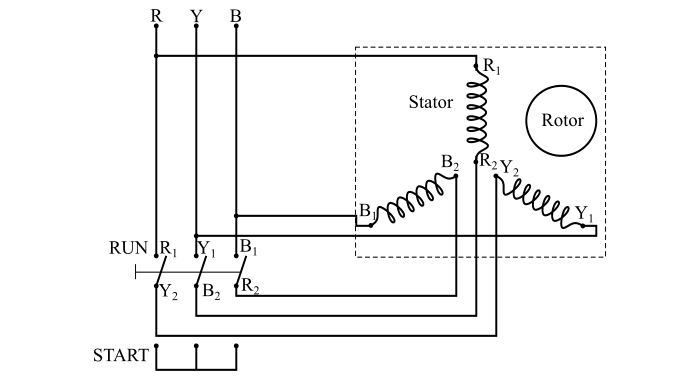
當開關 S 處於 START 位置時，定子繞組星形連線。當電機達到額定速度的約 80% 時，切換開關 S 切換到 RUN 位置，將定子繞組三角形連線。
透過首先將定子繞組星形連線，然後三角形連線，啟動時電機吸收的線路電流減少到三角形連線繞組啟動電流的三分之一。在啟動時，當定子繞組星形連線時，每個相位獲得的電壓等於 𝑉𝐿/√3，其中 VL 是線電壓。
由於非同步電動機的轉矩與施加電壓的平方成正比，因此與直接三角形啟動獲得的轉矩相比，星三角啟動器將啟動轉矩降低到三分之一。
星三角啟動器的理論
在啟動時，定子繞組以星形方式連線，因此每個相繞組上的電壓為
$$\mathrm{𝑉_1 =\frac{𝑉_𝐿}{\sqrt{3}}}$$
其中，
- VL = 線電壓
- V1 = 定子相電壓
假設，
𝐼𝑠𝑡.𝑌.𝑝ℎ = 定子繞組星形連線時的每相啟動電流
𝐼𝑠𝑡.𝑌.𝐿 = 定子繞組星形連線時的啟動線電流
此外，對於星形連線，線電流等於相電流，即
$$\mathrm{𝐼_{𝑠𝑡.𝑌.𝐿} = 𝐼_{𝑠𝑡.𝑌.𝑝ℎ}}$$
同樣，
𝐼𝑠𝑡.∆.𝑝ℎ = 定子繞組三角形連線時的每相啟動電流
𝐼𝑠𝑡.∆.𝐿 = 定子繞組三角形連線時的啟動線電流
𝐼𝑠𝑐.∆.𝑝ℎ = 定子繞組三角形連線時的短路相電流
𝑍𝑒10 = 電機在靜止狀態下折算到定子的每相等效阻抗
因此，定子繞組星形連線時的每相啟動電流由下式給出：
$$\mathrm{𝐼_{𝑠𝑡.𝑌.𝑝ℎ} =\frac{𝑉_1}{𝑍_{𝑒10}}=\frac{𝑉_𝐿}{\sqrt{3} 𝑍𝑒10}… (1)}$$
而定子繞組三角形連線時的每相啟動電流為
$$\mathrm{𝐼_{𝑠𝑡.∆.𝑝ℎ} =\frac{𝑉_𝐿}{𝑍_{𝑒10}}… (2)}$$
對於三角形連線，
$$\mathrm{線電流 = \sqrt{3} × 相電流}$$
$$\mathrm{⇒ 𝐼_{𝑠𝑡.∆.𝐿} = \sqrt{3} × 𝐼_{𝑠𝑡.∆.𝑝ℎ} =\frac{\sqrt{3} × 𝑉_𝐿}{𝑍_{𝑒10}}… (3)}$$
現在，取星三角啟動的啟動線電流與直接三角形切換的啟動線電流之比為
$$\mathrm{\frac{𝐼_{𝑠𝑡.𝑌.𝐿}}{𝐼_{𝑠𝑡.∆.𝐿}}=\frac{𝐼_{𝑠𝑡.𝑌.𝑝ℎ}}{𝐼_{𝑠𝑡.∆.𝐿}}=\frac{(𝑉_𝐿/\sqrt{3}𝑍_{𝑒10})}{\sqrt{3}(𝑉_𝐿/𝑍_{𝑒10})}=\frac{1}{3}}$$
⇒ 𝐼_{𝑠𝑡.𝑌.𝐿} = 𝐼_{𝑠𝑡.𝑌.𝑝ℎ} =\frac{1}{3}× 𝐼_{𝑠𝑡.∆.𝐿} … (4)
因此，使用星三角啟動器，來自主電源的啟動電流是直接三角形切換時啟動電流的三分之一。
此外，
$$\mathrm{\frac{Y − ∆ 啟動器的啟動轉矩}{直接三角形切換的啟動轉矩} =\frac{(𝑉_𝐿/\sqrt{3})^2}{𝑉_𝐿^2} =\frac{1}{3}… (5)}$$
因此，使用星三角啟動，啟動轉矩降低到直接三角形切換獲得的啟動轉矩的三分之一。
22K+ 次瀏覽
