編譯器設計中DFA的表示是什麼？

確定性意味著對於每個輸入，自動機都只有一個狀態可以從其當前狀態轉換。在確定性有限自動機中，磁頭只能向一個方向移動以掃描輸入帶上的符號。但在雙向有限自動機的情況下，在掃描輸入符號時，磁頭的移動方向可以向右或向左，從其當前位置移動。

確定性有限自動機是一組 5 元組，定義如下：

M = (Q, Σ, δ, q₀, F)

• Q：有限控制中存在的一組非空有限狀態 (q₀, q₁, q₂)。
• Σ：一組非空有限的輸入符號。
• δ：這是一個轉移函式，它接受兩個引數，一個狀態和一個輸入符號，它返回一個由 ∴ δ: Q x Σ → Q 表示的單個狀態。令 q 為傳遞給轉移函式的狀態，a 為輸入符號。δ(q, a) = q。q 是函式的輸出，它可能是相同的狀態或新狀態。
• $q_{0} \, \epsilon \, Q$ 是初始狀態。
• $F \subseteq Q$ 是最終狀態的集合。

有兩種方法可以表示確定性有限自動機：

• 狀態轉換圖

它是一個有向圖或流程圖，具有狀態和邊。狀態轉換圖由 John Myhill 於 1957 年建立。狀態轉換圖中的強路徑是一系列形成路徑的邊，從某個起始狀態開始，到某個最終狀態結束。它可以集中字母串，以便標記路徑中的每條邊。它可以生成被此機器接受的單詞。因此，它可以將狀態轉換圖描述為以下內容的集合：

• 一組有限的狀態，其中一個被命名為起始狀態，其中一些被命名為最終狀態。起始狀態用帶箭頭的圓圈表示，最終狀態用兩個同心圓表示。示意圖如下所示：

示例

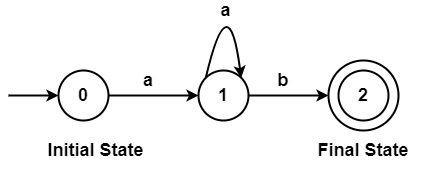
0、1、2→狀態

0→初始狀態

2→最終狀態

a、b→輸入符號

• 一個字母表 Σ，從中形成輸入字串的可能的輸入字母。

• 一組有限的轉換（標記邊），它顯示瞭如何根據讀取定義的輸入字母子字串從一個狀態轉換到另一個狀態。

• 狀態轉換表

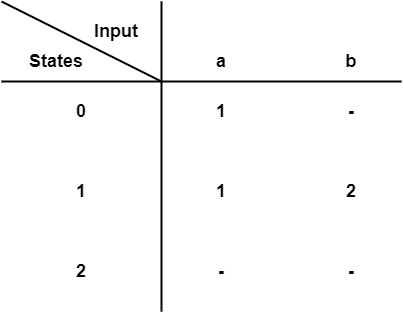
有限自動機可以用 5 元組 (Q, Σ, δ, q₀, F) 表示

• Q 是一組有限的非空狀態。
• Σ 是一組有限的輸入符號。
• $\delta$ 是轉移函式。
• q₀ ∈ Q 是初始狀態。
• F ⊆ Q 是最終狀態的集合。

示例 - 設計接受字串“abb”的有限自動機。

解決方案

狀態 - Q = {q₀, q₁, q₂, q₃}

輸入符號 - Σ = {a, b}

轉移函式 $\delta$ - {$\delta$(q₀, a) = q₁,$\delta$ (q₁, b) = q₂, $\delta$(q₂, b) = q₃}

初始狀態 - q₀

最終狀態 (F) - {q₃}

Ginni

更新於：2021年10月29日

2K+ 瀏覽量

開啟您的 職業生涯

透過完成課程獲得認證

開始學習