資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究在編譯器設計中，DFA 的最小化是什麼？
最小化意味著減少 DFA 中的狀態數。我們必須檢測 DFA 中那些存在或不存在都不會影響 DFA 接受的語言的狀態。這些狀態可以從 DFA 中消除。
演算法：DFA 的最小化
輸入 - DFA D1，具有一組狀態 Q 和一組終結狀態 F。
輸出 - DFA D2，它接受與 D1 相同的語言，並儘可能具有最少的狀態數。
方法
對狀態集進行劃分 'π'，分成兩個子集 -
- 終結狀態 'F'
- 非終結狀態 'Q-F'
∴ π={F,Q−F}
應用以下過程從 π 生成 πnew。
對於 π 中的每個集合 S
劃分 S 為子集，使得 S 中的兩個狀態 p 和 q 在 S 的同一個子集中，如果對於每個輸入符號 'a'，狀態 p 和 q 轉移到 π 的同一個集合中的狀態。它可以用形成的子集集替換 πnew 中的 S。
如果 πnew=π，則令 πfinal=π 並繼續執行步驟 4。否則對 π =πnew 重複步驟 2。
從 πfinal 的每個集合中選擇一個狀態作為該集合的代表。
這些狀態將是最小化 DFA D2 的狀態。
示例 1 - 將以下 DFA 轉換為最小化 DFA。
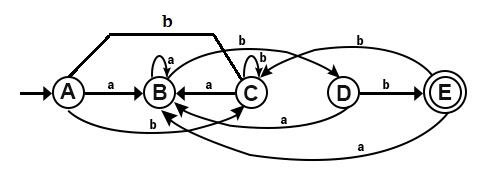
解決方案
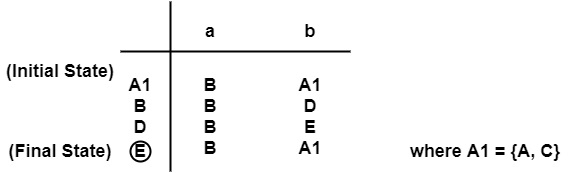
製作狀態轉換表
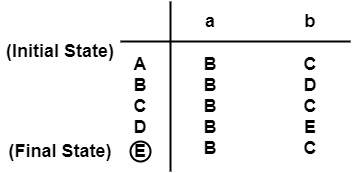
對狀態集進行劃分 'π'，即 π ={F,Q−F}
∴ π0={{E},{A,B,C,D}}
對於輸入符號 a，在 π0 的 {A, B, C, D} 上
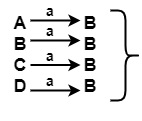
所有 B 都位於 π0 的同一集合 {A, B, C, D} 中
對於輸入符號 b，在 π0 的 {A, B, C, D} 上
∴ π0 的 {A,B,C,D} 將被拆分為 {A,B,C} 和 {D}
π1={{E},{A,B,C},{D}}
對於輸入 a，在 π1 的 {A, B, C} 上
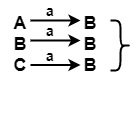
所有 B 都位於 π1 的同一集合中
對於輸入 b 在 π1 的 {A, B, C} 上
∴ π1 中的 {A,B,C} 將被拆分為 {A, C} 和 {B}
∴ π2={{E},{A,C},{B},{D}}
檢查 {A, C} 是否可以進一步拆分 (a)
- 對於輸入 a，在 π2 的 {A, C} 上
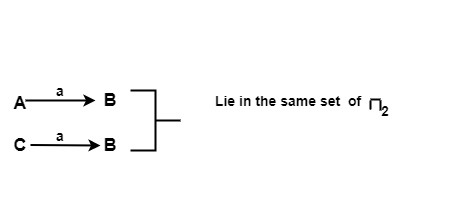
對於輸入 b，在 π2 的 {A, C} 上
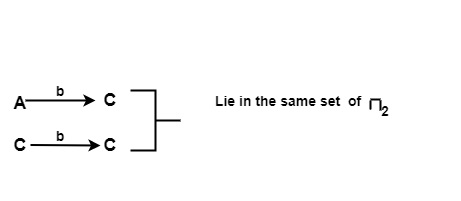
∴ {A,C} 不會被拆分
∴ π3={{E},{A,C},{B},{D}}
∴ π3=π2=πfinal={{E},{A,C},{B},{D}}
∴ 最小化 DFA 將有 4 個狀態，對應於給定 DFA 的 5 個狀態。
{A, C} 可以重新命名為 A1
B D E
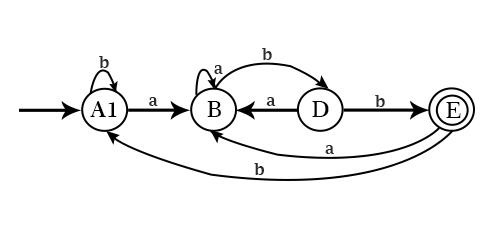
最小化 DFA 的狀態，即 A1、B、D、E 將透過檢視給定 DFA 表中的轉換連線起來。
最小化或簡化自動機將是
3K+ 次檢視
