資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究CRC 的計算演算法是什麼？
迴圈冗餘校驗 (CRC)
迴圈冗餘校驗 (CRC) 是一種由 W. Wesley Peterson 於 1961 年發明的分組碼。它通常用於檢測透過電信網路和儲存裝置傳輸的資料中意外發生的更改。
CRC 涉及將要傳送的資料位與通訊系統商定的預定除數進行二進位制除法。除數是使用多項式生成的。因此，CRC 也稱為多項式碼校驗和。
在透過網路通道傳送訊息之前，傳送方使用 CRC 對訊息進行編碼。接收方解碼傳入的訊息以檢測錯誤。如果訊息無錯誤，則接受該訊息；否則，接收方要求重新傳輸該訊息。
該過程說明如下
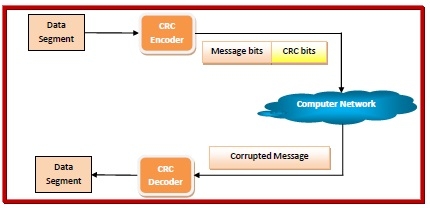
CRC 計算
當使用 CRC（多項式碼）對訊息進行編碼時，會使用一個稱為生成多項式 𝐺G(x) 的固定多項式。的值由傳送方和接收方共同商定。一個 k 位字由一個多項式表示，該多項式的範圍從 X0 到 xk-1。此多項式的階數是最高係數的冪，即 (K-1) G(x) 的長度應小於其編碼的訊息的長度。此外，其 MSB（最高有效位）和 LSB（最低有效位）都應為 1。在編碼過程中，CRC 位附加到訊息中，以便生成的幀可被 G(x) 整除。
使用 CRC 進行編碼的演算法
通訊雙方商定訊息的大小，M(x) 和生成多項式， G(x)。
如果 r 是 G(x) 的階數，則 r 位附加到 M(x) 的低階端。這使得塊大小為位，其值為 xrM(x)。
塊 xrM(x) 使用模 2 除法除以 G(x)。
除法後的餘數使用模 2 加法新增到 xrM(x) 中。結果是要傳輸的幀， T(x)。編碼過程使完全可被 G(x) 整除。
使用 CRC 進行解碼的演算法
接收方使用模 2 除法將傳入的資料幀 T(x) 單元除以 G(x)。在數學上，如果 E(x) 是錯誤，則執行 [M(x) + E(x)] 除以 G(x) 的模 2 除法。
如果沒有餘數，則表示 E(x)。接受資料幀。
餘數表示 E(x) 的非零值，換句話說，表示存在錯誤。因此，資料幀被拒絕。然後，接收方可能會向傳送方傳送錯誤確認以進行重傳。
6K+ 次檢視
