迪傑斯特拉演算法是什麼？

最短路徑路由演算法是一種廣泛使用的非自適應路由演算法，它根據迪傑斯特拉重要的最短路徑演算法來路由資料包。在這種方法中，到達節點的資料包會選擇網路中到特定目的地的最短路徑之一。

這種方法的缺點是它沒有充分考慮網路流量的變化。例如，排隊會在中間節點造成擁塞，導致資料包在到達目的地之前被延遲。在這種情況下，最好讓資料包選擇可能不是最短路徑但最終可以更快傳輸時間的路徑。

最短路徑路由 (SPR) 演算法根據網路中各種矩陣表示的成本度量來評估路由。

設 V 為有向圖的所有邊的集合，C[S, V] 為到任何待評估節點的最少成本（最短路徑）矩陣。最初，在新增其路由之前，每條邊（節點）將到任何其他邊的最短路徑成本設定為無窮大，即 ∞。假設有向圖中有 n 條邊，每條邊都透過選擇其鄰居 x（屬於 V – S）來評估到不同節點的最短路徑成本，該鄰居 x 從 S 到 x 的權重 W 值最低。它使用以下公式評估每條邊 (S, x)（S 的鄰居）的路由。

D [V] = min (D [V], D [V] + C(S, V))

C (S, V) 是連線到 S 的頂點的成本。此過程一直持續到訪問所有有向圖邊為止。當演算法中斷時，網路中的所有節點都必須找到每個節點的最短路徑。

演算法步驟

• 源節點被初始化並用黑色圓圈表示。

• 確定相鄰節點的成本，並將其重新標記為源節點。

• 透過檢查相鄰節點來確定最小標籤，使其永久化並將其作為源節點。

例如，我們想從 A 獲取 G。步驟如下：

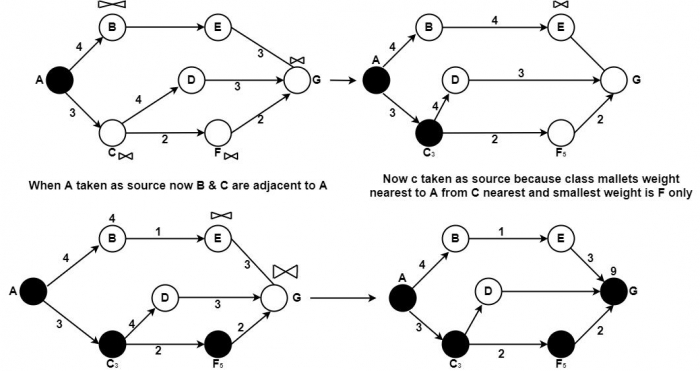
首先將 A 作為第一個源節點並將其加黑。然後是 C，然後是 F，G 離 F 最近，到達目的地的總權重為 7（從 A 到 G），最短路徑是 (A, C, F, G)，而不是 ABEG。

Ginni

更新於：2021年5月5日

瀏覽量：572

開啟您的職業生涯

完成課程獲得認證

開始學習