資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究頂點覆蓋
覆蓋圖是一個子圖，它包含所有頂點或與某個其他圖對應的所有邊。包含所有頂點的子圖稱為線/邊覆蓋。包含所有邊的子圖稱為頂點覆蓋。
設 'G' = (V, E) 為一個圖。V 的一個子集 K 稱為 'G' 的頂點覆蓋，如果 'G' 的每條邊都與 K 中的一個頂點關聯或被 K 中的一個頂點覆蓋。
示例
檢視以下圖形 -
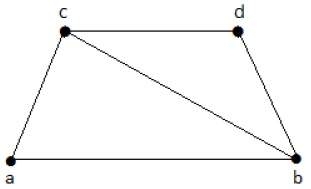
從上圖可以匯出的子圖如下 -
K1 = {b, c}
K2 = {a, b, c}
K3 = {b, c, d}
K4 = {a, d}這裡，K1、K2 和 K3 有頂點覆蓋，而 K4 沒有頂點覆蓋，因為它沒有覆蓋邊 {bc}。
最小頂點覆蓋
如果圖 'G' 的頂點 'K' 不能刪除任何頂點，則稱其為最小頂點覆蓋。
示例
在上圖中，具有頂點覆蓋的子圖如下 -
K1 = {b, c}
K2 = {a, b, c}
K3 = {b, c, d}
這裡，K1 和 K2 是最小頂點覆蓋，而在 K3 中，可以刪除頂點 'd'。
最小頂點覆蓋
也稱為最小的最小頂點覆蓋。具有最少頂點數的圖 'G' 的最小頂點覆蓋稱為最小頂點覆蓋。
'G' 的最小頂點覆蓋中的頂點數稱為 G 的頂點覆蓋數 (α2)。
示例
在下圖中，具有頂點覆蓋的子圖如下 -
K1 = {b, c}
K2 = {a, b, c}
K3 = {b, c, d}
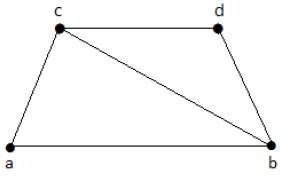
這裡，K1 是 G 的最小頂點覆蓋，因為它只有兩個頂點。α2 = 2。
更新於: 2020年1月21日
233 次檢視
廣告