資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究圖的割集和割頂
是否能夠從一個頂點遍歷到圖中的另一個頂點取決於圖的連線方式。連通性是圖論中的一個基本概念。連通性定義了圖是連通的還是不連通的。
連通性
如果每對頂點之間都存在一條路徑，則稱該圖是連通的。從每個頂點到任何其他頂點，都應該存在一些路徑可以遍歷。這稱為圖的連通性。具有多個不連通頂點和邊的圖稱為不連通圖。
割頂
設 'G' 為一個連通圖。如果 'G-V'（從 'G' 中刪除 'V'）導致一個不連通圖，則頂點 V ∈ G 稱為 'G' 的割頂。從圖中移除一個割頂會將其分成兩個或多個圖。
注意 - 刪除割頂可能會使圖變得不連通。
一個連通圖 'G' 最多可以有 (n–2) 個割頂。
示例
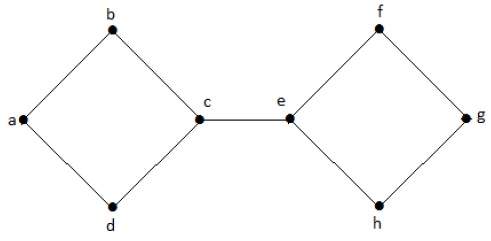
在下圖中，頂點 'e' 和 'c' 是割頂。
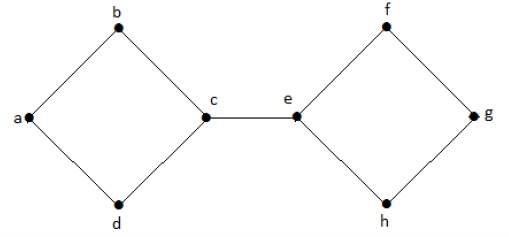
透過移除 'e' 或 'c'，該圖將變成一個不連通圖。
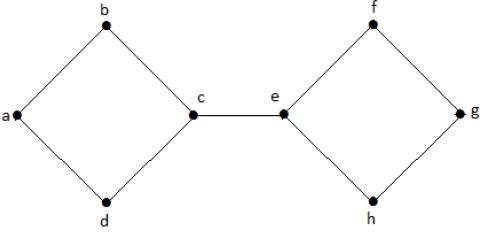
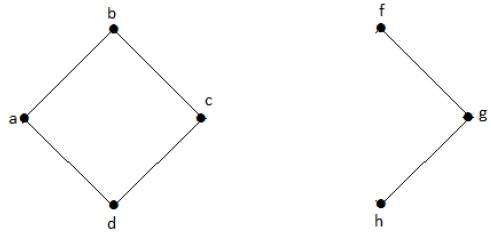
如果沒有 'g'，則頂點 'c' 和頂點 'h' 以及許多其他頂點之間沒有路徑。因此，它是一個不連通圖，其割頂為 'e'。類似地，'c' 也是上圖的割頂。
割邊（橋）
設 'G' 為一個連通圖。如果 'G-e' 導致一個不連通圖，則邊 'e' ∈ G 稱為割邊。
如果從圖中移除一條邊會導致兩個或多個圖，則該邊稱為割邊。
示例
在下圖中，割邊為 [(c, e)]
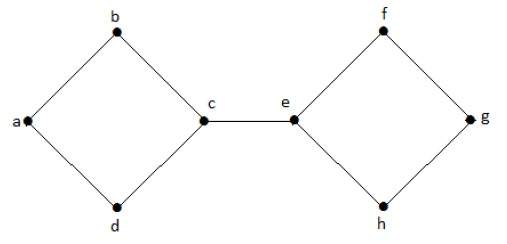
從圖中移除邊 (c, e) 後，它將變成一個不連通圖。
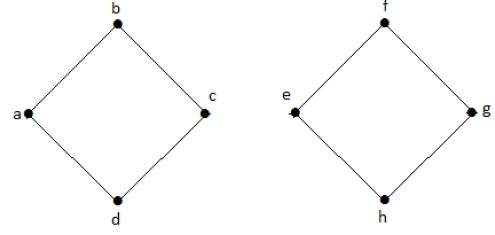
在上圖中，移除邊 (c, e) 將圖分成兩部分，這實際上是一個不連通圖。因此，邊 (c, e) 是該圖的割邊。
注意 - 設 'G' 為一個具有 'n' 個頂點的連通圖，則
邊 e ∈ G 是割邊當且僅當邊 'e' 不屬於 G 中的任何環。
可能的割邊最大數量為 'n-1'。
只要存在割邊，也一定存在割頂，因為割邊的至少一個頂點是割頂。
如果存在割頂，則割邊可能存在也可能不存在。
圖的割集
設 'G'= (V, E) 為一個連通圖。如果從 G 中刪除 E' 中的所有邊使 G 不連通，則 E 的子集 E' 稱為 G 的割集。
如果從圖中刪除一定數量的邊使其不連通，則這些被刪除的邊稱為該圖的割集。
示例
看一下下圖。它的割集是 E1 = {e1, e3, e5, e8}。
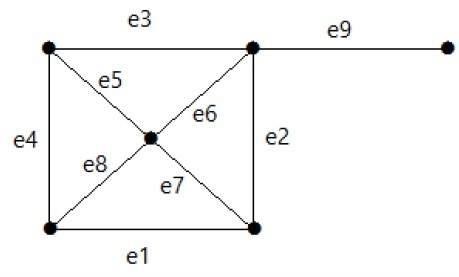
從圖中移除割集 E1 後，它將顯示如下 -
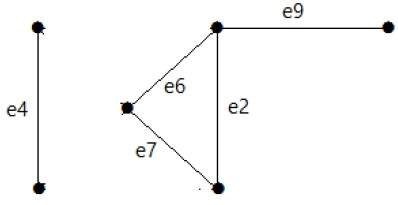
同樣，還有其他可以使圖不連通的割集 -
- E3 = {e9} - 圖中最小的割集。
- E4 = {e3, e4, e5}
35K+ 瀏覽量
