JavaScript中的樹遍歷

Javascript Web開發前端技術

樹是一種非線性的分層資料結構，它結合了**節點**和**邊**。樹中的節點儲存值，這些節點透過**邊**相互連線。樹的最頂層節點沒有任何父節點，被稱為根節點。

下面的二叉搜尋樹用重要術語進行了標記。

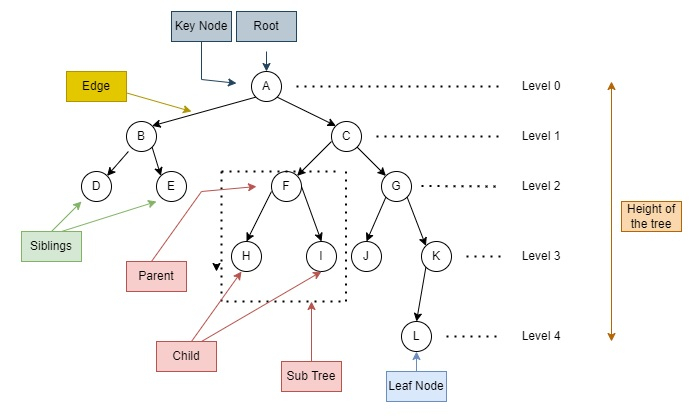
基本術語

**節點** - 指向另一個節點的指標，並能夠儲存任何資料型別的數值。
**根** - 此節點位於樹的最頂部，沒有父節點。
**子節點** - 子節點是直接與其對應的父節點連線的節點。
**邊** - 樹的邊是連線兩個節點的連結。
**路徑** - 沿著樹的邊的節點順序稱為其路徑。
**父節點** - 父節點具有附加為子樹的子節點。
**葉子節點** - 沒有任何子節點附加到它的節點。
**子樹** - 它是樹的一個較小的部分，將內部節點視為其根，並將所有連線到它的路徑視為子節點。
**遍歷** - 以特定順序遍歷樹中的每個節點。
**層級** - 從節點到其根節點的後代數量稱為層級。
**樹的高度** - 從根到葉子的路徑。它被定義為子樹的最大高度 + 1。

樹遍歷資料結構

一般來說，“遍歷”這個詞意味著“穿過（或穿過）”。樹遍歷是在我們訪問樹的每個節點的操作。

樹中有多種型別的遍歷技術：

**中序遍歷** - 透過訪問左子樹、根節點，然後右子樹（在BST中）遞迴遍歷樹的過程稱為中序遍歷。這種遍歷也稱為對稱遍歷。

左 → 根 → 右
**前序遍歷** - 在這種遍歷中 - 首先遍歷根節點，然後遞迴遍歷左子樹和右子樹的過程。字首遍歷也是用來描述這個過程的術語。

根 → 左 → 右
**後序遍歷** - 遞迴地遍歷左節點、右節點，然後根節點的過程。字尾遍歷是這種遍歷的另一個名稱。

左 → 右 → 根

我們總是從根（頭部）節點開始，因為所有節點都透過邊（連結）連線。在其他情況下，我們無法隨機訪問樹節點。

BST遍歷的實現

在下面的指令碼中，我們以獨特的方式實現了所有三種遍歷。

示例


<! DOCTYPE html>
<html>
   <head>
      <script>
         class Node {
            constructor(value) {
               this.value = value;
               this.left = null;
               this.right = null;
            }
         }
         class BinarySearchTree {
            constructor() {
               this.root = null;
            }

            inserting(value) {
               let node = new Node(value);
               if(this.root == null) {
                  this.root = node;
               }else {
                  this.insertNode(this.root, node);
               }
            }

            insertNode(root, newNode) {
               if(newNode.value < root.value) {
                  if(root.left == null) {
                     root.left = newNode;
                  } else {
                     this.insertNode(root.left, newNode);
                  }
               } else if(newNode.value > root.value) {
                  if(root.right == null) {
                     root.right = newNode;
                  } else {
                     this.insertNode(root.right, newNode);
                  }
               }
            }
            getRootNode() {
               return this.root;
            }

            /* implementation of individual operations of traversal in tree */

            preorderTrav(root) {
               if(root != null) {
                  document.write(root.value); // Traverse the root node
                  this.preorderTrav(root.left); /* Traverse the left subtree */
                  this.preorderTrav(root.right); /* Traverse the right subtree */
               }
            }

            inorderTrav(root) {
               if(root != null) {
                  this.inorderTrav(root.left); /* Traverse the left subtree */
                  document.write(root.value); // Traverse the root node
                  this.inorderTrav(root.right); /* Traverse the right subtree */
               }
            }

            postorderTrav(root) {
               if(root != null) {
                  this.postorderTrav(root.left); /* Traverse the left subtree */
                  this.postorderTrav(root.right); /* Traverse the right subtree */
                  document.write(root.value); // Traverse the root node
               }
            }
         }
         
         var bst = new BinarySearchTree();
         bst.inserting(30);
         bst.inserting(50);
         bst.inserting(20);
         bst.inserting(14);
         bst.inserting(44);
         bst.inserting(34);
         bst.inserting(26);
         bst.inserting(10);
         bst.inserting(19);
         bst.inserting(54);
         
         var root = bst.getRootNode();
         document.write("preorder traversal of the binary tree is <br>");
         bst.preorderTrav(root);
         document.write('<br>');
         document.write('inorder traversal of the binary tree is <br>');
         bst.inorderTrav(root);
         document.write('<br>');
         document.write('Postorder traversal of the binary tree is <br>');
         bst.postorderTrav(root);
         document.write('<br>');
      </script>
   </head>
   <body>
   </body>
</html>

輸出

上述指令碼的輸出將是：

Pre-order traversal of the binary tree is
30 20 14 10 19 26 50 44 34 54

In-order traversal of the binary tree is
10 14 19 20 26 30 34 44 50 54

Post-order traversal of the binary tree is
10 19 14 26 20 34 44 54 50 30

Nikhilesh Aleti

更新於：2022年11月18日

2K+ 次瀏覽

啟動您的職業生涯

透過完成課程獲得認證

開始