資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚學
法學圖的傳遞閉包
傳遞閉包是圖中從頂點 u 到頂點 v 的可達矩陣。給定一個圖，對於所有頂點對 (u, v)，我們必須找出可以從另一個頂點 u 到達的頂點 v。
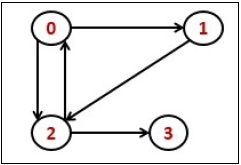
最終矩陣是布林型別。當從頂點 u 到頂點 v 出現值 1 時，則表示從 u 到 v 至少有一條路徑。
輸入和輸出
Input: 1 1 0 1 0 1 1 0 0 0 1 1 0 0 0 1 Output: The matrix of transitive closure 1 1 1 1 0 1 1 1 0 0 1 1 0 0 0 1
演算法
transColsure(graph)
輸入：給定的圖。
輸出：傳遞閉包矩陣。
Begin copy the adjacency matrix into another matrix named transMat for any vertex k in the graph, do for each vertex i in the graph, do for each vertex j in the graph, do transMat[i, j] := transMat[i, j] OR (transMat[i, k]) AND transMat[k, j]) done done done Display the transMat End
<2>示例
#include<iostream>
#include<vector>
#define NODE 4
using namespace std;
/* int graph[NODE][NODE] = {
{0, 1, 1, 0},
{0, 0, 1, 0},
{1, 0, 0, 1},
{0, 0, 0, 0}
}; */
int graph[NODE][NODE] = {
{1, 1, 0, 1},
{0, 1, 1, 0},
{0, 0, 1, 1},
{0, 0, 0, 1}
};
int result[NODE][NODE];
void transClosure() {
for(int i = 0; i<NODE; i++)
for(int j = 0; j<NODE; j++)
result[i][j] = graph[i][j]; //initially copy the graph to the result matrix
for(int k = 0; k<NODE; k++)
for(int i = 0; i<NODE; i++)
for(int j = 0; j<NODE; j++)
result[i][j] = result[i][j] || (result[i][k] && result[k][j]);
for(int i = 0; i<NODE; i++) { //print the result matrix
for(int j = 0; j<NODE; j++)
cout << result[i][j] << " ";
cout << endl;
}
}
int main() {
transClosure();
}輸出
1 1 1 1 0 1 1 1 0 0 1 1 0 0 0 1
更新時間：16-6-2020
17K+ 瀏覽量
廣告