資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會研究
服裝研究
法律研究斯溫伯恩直流電機測試——直流電機測試
斯溫伯恩測試是一種間接測試直流電機的測試方法，以詹姆斯·斯溫伯恩爵士命名。在這種方法中，損耗是分開確定的，並且預先確定了所需負載下的效率。斯溫伯恩測試是測試具有恆定磁通的並勵和復勵直流電機的最簡單方法。
連線圖如圖所示，電機在額定電壓和速度下作為電動機執行。
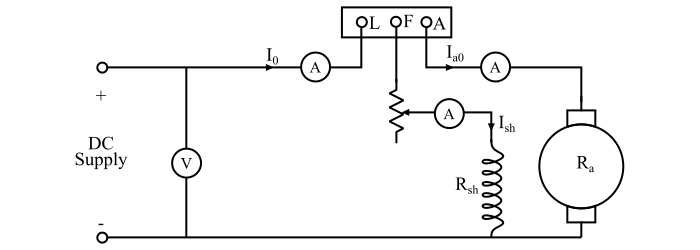
假設：
$$V = 供電電壓$$
$$I_0 = 空載線電流$$
$$I_{sh} = 並勵繞組電流$$
$$因此，空載電樞電流，I_{a0} = I_0 - I_{sh}$$
以及
$$空載輸入功率 = VI_0$$
該電機的空載輸入功率提供以下各項：
- 鐵損
- 空載電樞銅損
- 摩擦和風損
在空載情況下，電機的有用機械輸出為零，因此空載輸入功率僅用於補償電機中的損耗。因此，
$$空載電樞銅損 = (I_{a0})^2R_a$$
其中，Ra是電樞繞組的電阻。
因此，電機中的恆定功率損耗將為：
$$P_C = 空載輸入功率 - 空載電樞銅損$$
$$⇒ P_C = VI_0 - (I_{a0})^2R_a$$
現在，在知道電機的恆定損耗後，可以如下確定其在任何其他負載下的效率：
假設“I”是需要計算電機效率的負載電流。
作為電動機執行時的效率
這裡：
$$電樞電流，I_a = I - I_{sh}$$
$$電動機輸入功率 = VI$$
$$電樞銅損 = I_a^2R_a = (I - I_{sh})^2R_a$$
$$因此，電機中的總損耗 = (I - I_{sh})^2R_a + P_C$$
其中，PC是上面確定的恆定損耗。
因此，
$$電動機效率，η_m = 輸出/輸入 = (輸入 - 損耗)/輸入$$
$$⇒ η_m = \frac{VI - (I - I_{sh})^2R_a - P_C}{VI}$$
作為發電機執行時的效率
這裡：
$$電樞電流，I_a = I + I_{sh}$$
$$發電機輸出功率 = VI$$
$$電樞銅損 = I_a^2R_a = (I + I_{sh})^2R_a$$
$$因此，電機中的總損耗 = (I + I_{sh})^2R_a + P_C$$
$$發電機效率，η_g = 輸出/(輸出 + 損耗) = \frac{VI}{VI + (I + I_{sh})^2R_a + P_C}$$
斯溫伯恩測試的優點
以下是斯溫伯恩測試的優點：
- 測試大型電機所需的功率非常小，因此這是一種經濟且方便的直流電機測試方法。
- 由於已知恆定損耗，因此可以預先確定任何負載下的效率。
斯溫伯恩測試的缺點
斯溫伯恩測試的主要缺點是：
- 沒有考慮從空載到滿載的鐵損變化。在滿載時，由於電樞反應，磁通發生畸變，從而增加了鐵損。
- 由於斯溫伯恩測試是在空載下進行的，因此它不能指示滿載時的換向是否令人滿意，以及溫升是否在規定的限值內。
斯溫伯恩測試的侷限性
斯溫伯恩測試具有以下侷限性：
- 斯溫伯恩測試僅適用於磁通實際上恆定的直流電機，即並勵電機和平復勵發電機。
- 串勵直流電機不能用斯溫伯恩測試進行測試，因為它們不能在空載下執行，並且它們的磁通和速度變化很大。
6K+ 次瀏覽
