統計物理學

---

介紹

統計物理學是物理學的一個分支，它為人們提供了許多實用的模型。統計物理學利用統計學和機率論的方法。這些數學工具尤其有助於處理大量群體和解決物理學問題。統計物理學有助於闡明具有內在隨機性的廣泛領域。統計物理學的主要目的是闡明物質的特性，以及支配原子運動的物理定律。統計物理學闡明並定量地討論了超流性、湍流、超導性、等離子體和固體中的集體現象以及液體的結構特性。

什麼是統計物理學？

統計物理學的目標是根據平衡態下系統的宏觀因素來了解系統。它是透過力學定律從微觀粒子的性質資訊中推匯出來的 (Kolchinsky & Wolpert, 2018)。這個過程與熱力學不同，熱力學是從微觀粒子的平衡態來診斷系統的宏觀引數，而不是觀察微觀粒子的引數。

圖片即將推出

統計方法被定義為系統被放置在確定自由能的劃分中。統計物理學基於微觀定律的資料來處理原子運動和物理定律的剩餘部分 (Gorban & Tyukin, 2018)。統計物理學有助於學習熱平衡態和非平衡態。統計學的應用有助於解釋像布朗運動這樣的隨機過程，比如熱力學。

統計描述的必要性是什麼？

統計描述被定義為簡潔的描述性係數，總結了一組給定的資料，這組資料可以是總體樣本或整個總體的代表。正如Hou & Huang (2020)所述，描述性統計學被分解成計算變異性和集中趨勢。以研究玻璃為例，研究並獲得了粒子的速度的統計分佈，從而理解宏觀可見特性（如溫度、體積和壓力）之間的關係。

統計描述提供了對更好理解和精確描述的重要見解。物理學的一個分支是測量自由能的特定方案（Kolchinsky & Wolpert, 2018）。在理解統計物理學中，統計力學結合了統計學與熱力學領域的原理和方法。在物理學中，主要關注統計描述，以使對粒子的研究比描述性研究更詳盡。

量子和數學統計物理學的分析

在現代物理學中，量子統計物理學或量子統計力學是指應用於量子力學系統的統計力學。密度算符表示量子力學中量子可能態上的統計系綜或機率分佈，它是一個自伴的、跡類算符，在描述量子系統的希爾伯特空間上是非負的且跡為1。事實證明，量子物理學不需要超越統計學的概念 (Azha et al. 2018)。這些區別只是表面的，經典統計系統特性的結果有助於理解量子力學的描述。量子統計學是與相同基本粒子、原子和離子的數量在量子可能態之間的區別相關的統計學。

數學中的統計物理學表示為統計力學。它由J. Willard Gibbs在1902年提出。統計系綜被稱為包含大量系統虛擬副本的集合，所有這些副本都是同時計算的。統計系綜中的每一個都代表了真實系統可能發生的一種狀態。基本的機率論關注統計物理學的數學方面 (Luginbuhl, Rundle & Turcotte, 2019)。一些關於機率分佈、排列、方差和均值的概念依賴於數學統計物理學。

統計物理學的應用

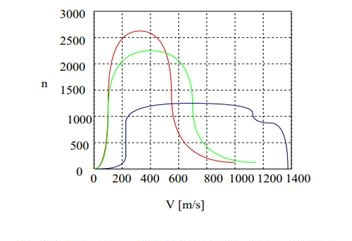
統計物理學有助於深入瞭解廣泛的過程範圍，如擴散。正如Ray (2019)所述，將統計方法應用於熱力學可能導致對熵和溫度等概念的深入理解。例如，溫度在統計上被理解為大塊材料中原子平均動能。統計物理學的應用如下所示。

• 主要統計物理學的應用集中在分子在集合中的分佈。統計物理學在麥克斯韋分子速度分佈中非常有用。

• 如果溫度高，粒子密度低。

• Gibbs 強調了熱力學及其其他方面在統計物理學中的事實。

結論

在固態物理學中，統計物理學支援對關鍵狀態、相變和液晶的研究。在工程或物理學的研究中，統計學更可行，力學更受青睞。統計物理學在這兩門學科中都具有很強的互補性。統計物理學相對容易，然而，與物理學相比，物理學需要快速運用智商。在物理學中，統計描述有助於構建對特定領域的統計研究的有效和適當的計劃。統計物理學已被證明有利於推導量子物理學的路徑積分公式。

常見問題

Q.1. 統計力學的主要假設是什麼？

A. 這個假設通常被稱為等機率原理，它基於機率論。它指出，如果微觀態具有相同的能量，那麼在系綜中，粒子數和體積數出現的頻率是相同的。

Q.2. 統計物理學的主要應用是什麼？

A. 統計物理學的形式化使能夠將一般結果應用於不同的分支，如經濟學、生物學和固態理論。統計物理學在實際生活中的應用非常有趣。

Q.3. 統計物理學的型別有哪些？

A. 理想氣體的統計力學、熵、量子統計、輻射應用等等都是統計物理學的基本概念。統計學提供了高度的自由度來自成形的概念。

Q.4. 熱力學和統計力學有什麼區別？

A. 統計力學或物理學是指從基本粒子之間微觀力的資料出發，對宏觀系統的物理行為進行研究的概念。另一方面，熱力學是指系統不同宏觀可見性（如壓力、溫度、極化和磁化）之間關係的概念。