資料結構中虛擬樹中的伸展樹

在虛擬樹中，一些邊被視為實線，一些被視為虛線。通常的伸展操作只在實線樹中執行。為了在虛擬樹中的節點 y 上執行伸展操作，實現了以下方法。

該演算法檢視樹三次，每次遍歷一次，並對其進行更改。在第一次遍歷中，僅在實線樹中執行伸展操作，從節點 y 開始，從 y 到整個樹根的路徑變為虛線。這條路徑透過拼接變為實線。現在，在節點 y 上進行最終的伸展操作將使 y 成為樹的根。非正式地說，該演算法解釋如下

伸展(y) 演算法

第一遍 沿著虛擬樹向上遍歷，但伸展操作僅在實線子樹內執行。在這一遍結束時，從 y 到根的路徑變為虛線。

第二遍 從節點 y 向上遍歷，在 y 的每個真祖先節點處進行拼接。在這一步結束時，從 y 到根的路徑變為實線。除此之外，節點 y 及其在原始樹（第一遍之前的樹）中的所有子節點現在都成為左子節點。

第三遍 從節點 y 向上遍歷到根，以正常方式執行伸展操作。

這使我們能夠利用先驗知識來改進我們的機率估計。對於給定的葉子集。因此，目標是構建一個具有最小外部路徑權重的樹。

下面給出一個例子

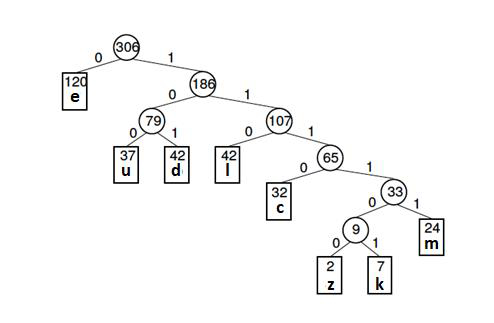
字母頻率表

霍夫曼編碼

霍夫曼樹（以上例為例）如下所示

Arnab Chakraborty

更新於: 2020-01-07

138 次檢視

開啟你的 職業生涯

透過完成課程獲得認證

立即開始