資料結構中紅黑樹的插入

紅黑樹是一種自平衡二叉搜尋樹，其中樹的每個節點都著色為紅色或黑色。我們可以在紅黑樹上執行三種類型的操作——搜尋、插入和刪除。

假設我們必須在以下紅黑樹中插入一個元素。

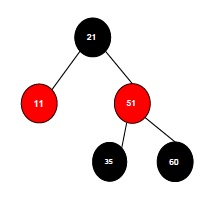
在紅黑樹中插入元素的想法非常簡單——我們就像在普通二叉樹中插入一樣進行插入。我們從根節點開始，檢查節點的顏色，並將其插入特定位置。但是，在紅黑樹中，應該有一些額外的程式來插入元素。

但是，我們應該知道，當紅黑樹滿足以下條件時，它是平衡的：

  • 每個根節點必須是黑色的。

  • 每個節點要麼是紅色，要麼是黑色。

  • 如果一個節點是紅色的，那麼它的子節點必須是黑色的。

  • 從根到末端的路徑必須包含相同數量的黑色節點。

如果我們想在紅黑樹中插入一個新節點，那麼我們可以透過檢視插入步驟來實現。

在紅黑樹中插入元素的步驟：

  • 檢查樹是否為空。如果樹為空，則插入一個新節點並將其顏色設定為黑色。（因為根節點必須始終為黑色）

  • 否則，如果樹不為空，則將新節點作為葉節點插入到末尾，並將其顏色設定為紅色。

  • 如果新節點的父節點為紅色，並且其相鄰（父節點的）節點也為紅色，則翻轉兩個相鄰節點和父節點以及祖父母節點（如果它不是根節點，否則只翻轉父節點和相鄰節點的顏色）的顏色，即黑色。

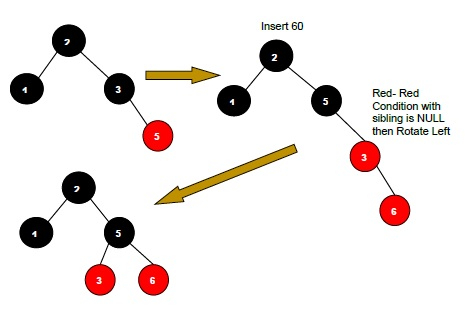
  • 如果新節點的父節點為紅色，並且其相鄰（父節點的）節點為空或為 NULL，則旋轉（左左或左右旋轉）新節點和父節點。

有兩種型別的旋轉適用 - 左左旋轉和左右旋轉。旋轉僅在某些條件下適用。條件是：

  • 如果新節點的父節點為紅色，並且相鄰節點為空或為 NULL，則進行左旋轉或右旋轉。

  • 在左左旋轉中，翻轉父節點和祖父母節點的顏色。將父節點設為祖父母節點，並將祖父母節點設為子節點。


演算法

RBTreeInsertion(root,key)

//The color of the inserted new node is Red
color[key] <- Red
while(key≠root and color (p[key]=Red))
do if p[key]= left(p[p[key]])
   Then y←right[p[p[key]]
// If the parent of the new node is Red(if there is Grandparent instead
root Node) Flip the color.
   if color[y]← Red
   then color(p[key])← Black
      color(p[p[key]])← Red
      key← p[p[key]]
   else if key← right[p[key]]
      then key← p[key]
      //When parent of new node has the red color and its sibling is NULL
   LeftRotate(root,key)
   color(p[key]) ← Black
   color(p[p[key]]) ← Red
RotateRight(root,p[p[key]])
else exchange then left and right elements to make it balance.
color(root)← Black

更新於: 2021年2月5日

7K+ 瀏覽量

開啟你的 職業生涯

透過完成課程獲得認證

開始學習
廣告