資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究集合運算
維恩圖由約翰·維恩於1880年發明，是一種示意圖，顯示不同數學集合之間所有可能的邏輯關係。
示例
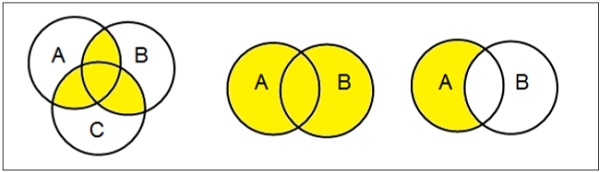
集合運算
集合運算包括集合並集、集合交集、集合差、集合補集和笛卡爾積。
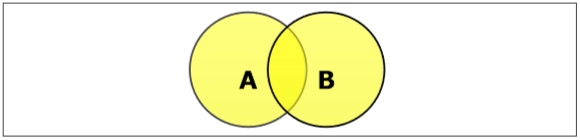
集合並集
集合 A 和 B 的並集（用 A ∪ B 表示）是屬於 A、屬於 B 或同時屬於 A 和 B 的元素的集合。因此，A ∪ B = { x | x ∈ A 或 x ∈ B }。
示例 - 如果 A = { 10, 11, 12, 13 } 且 B = { 13, 14, 15 }，則 A ∪ B = { 10, 11, 12, 13, 14, 15 }。（公共元素只出現一次）
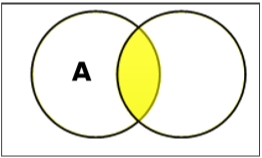
集合交集
集合 A 和 B 的交集（用 A ∩ B 表示）是同時屬於 A 和 B 的元素的集合。因此，A ∩ B = { x | x ∈ A 且 x ∈ B }。
示例 - 如果 A = { 11, 12, 13 } 且 B = { 13, 14, 15 }，則 A ∩ B = { 13 }。
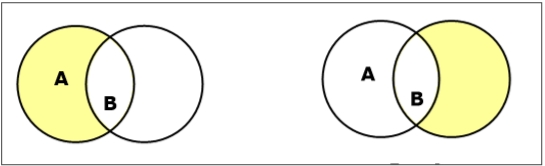
集合差/相對補集
集合 A 和 B 的集合差（用 A – B 表示）是僅屬於 A 但不屬於 B 的元素的集合。因此，A - B = { x | x ∈ A 且 x ∉ B }。
示例 - 如果 A = { 10, 11, 12, 13 } 且 B = { 13, 14, 15 }，則 (A - B) = { 10, 11, 12 } 且 (B - A) = { 14, 15 }。在這裡，我們可以看到 (A - B) ≠ (B - A)
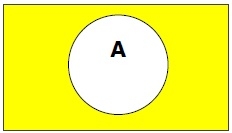
集合補集
集合 A 的補集（用 A' 表示）是不屬於集合 A 的元素的集合。因此，A' = { x | x ∉ A }。
更具體地說，A'= (U - A)，其中U 是包含所有物件的全集。
示例 - 如果 A = { x | x 屬於奇數集合 }，則 A' = { y | y 不屬於奇數集合 }
笛卡爾積/叉積
n 個集合 A1、A2、... An 的笛卡爾積表示為 A1 × A2 ... × An，可以定義為所有可能的序對 (x1、x2、... xn)，其中 x1 ∈ A1、x2 ∈ A2、... xn ∈ A_n
示例 - 如果我們取兩個集合 A = { a, b } 和 B = { 1, 2 }，
A 和 B 的笛卡爾積寫成 - A × B = { (a, 1), (a, 2), (b, 1), (b, 2)}
B 和 A 的笛卡爾積寫成 - B × A = { (1, a), (1, b), (2, a), (2, b)}
8K+ 瀏覽量
