矩形稜錐

---

簡介

矩形稜錐是一種三維立體圖形，具有矩形底面和四個三角形平面。根據底面的形狀和三角形面的數量，稜錐有很多種型別，例如正方形稜錐、三角形稜錐、五邊形稜錐和六邊形稜錐。

稜錐的表面是具有直線的平面圖形，也可以稱為多邊形。

如果一個立體圖形由多邊形構成，則稱為多面體。矩形稜錐，或一般意義上的稜錐，都是多面體。稜錐的一種常見型別是矩形稜錐。埃及的金字塔可以作為矩形稜錐的現例項子。埃及人是最早測量稜錐體積的人。

在本教程中，我們將學習如何在不同場景下計算矩形稜錐的表面積和體積。

矩形稜錐

具有五個頂點和八條直線，形成四個三角形表面和一個矩形底面的立體圖形稱為矩形稜錐。

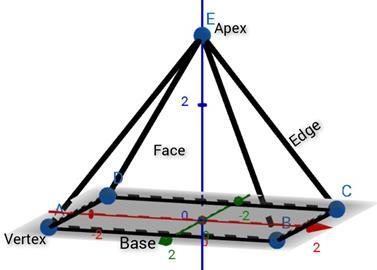
• 連線所有三角形表面的頂部尖端或點被稱為矩形稜錐的頂點。

• 其餘的點或角，作為邊其他端點的交點，是頂點。

• 由側面交點形成的直線是稜。

• 圖形的底面和其他表面是面。

表面積公式

當我們探索矩形稜錐的表面積時，我們需要考慮總表面積和側表面積。

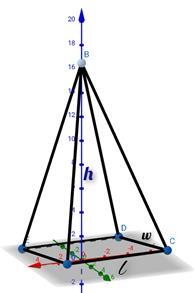
矩形稜錐的總表面積

側表面積和底面積之和是矩形稜錐的總表面積或 TSA。

公式如下：

$$\mathrm{T.S.A\:=\:lw\:+\:l\sqrt{[(\frac{W}{2})^{2}\:+\:h^{2}]}\:+\:w\sqrt{[(\frac{l}{2})^{2}}\:+\:h^{2}]}$$

其中 l 為底邊長

w 為底邊寬

h 為稜錐的高度

矩形稜錐的側表面積

不包括底面積的所有側三角形面的面積之和是矩形稜錐的側表面積或 LSA。

公式如下：$$\mathrm{L.S.A\:=\:l\sqrt{[(\frac{W}{2})^{2}\:+\:h^{2}]}\:+\:w\sqrt{[(\frac{l}{2})^{2}}\:+\:h^{2}]}$$

其中 l 為底邊長

w 為底邊寬

h 為稜錐的高度

矩形稜錐體積公式

矩形稜錐的體積是透過將底面積 B 乘以稜錐的垂直高度 h 來計算的。

公式如下

$\mathrm{volume\:V\:=\:\frac{1}{3}\times\:base\:are\:\times\:perpendicular\:height}$

$\mathrm{V\:=\:\frac{1}{3}\:Bh}$

$\mathrm{V\:=\:\frac{1}{3}\times\:l\times\:w\times\:h}$

其中底面積 B 為 lw

l 為底邊長

w 為底邊寬

h 為稜錐的垂直高度。

例題

1)在文員的辦公桌上有一個紙鎮，形狀為矩形稜錐，高 5 釐米，底寬 4 釐米，底長 6 釐米。求紙鎮的總表面積。

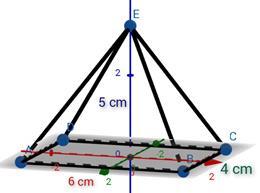
答案 −

矩形稜錐的總表面積

$$\mathrm{=\:lw\:+\:l\sqrt{[(\frac{W}{2})^{2}\:+\:h^{2}]}\:+\:w\sqrt{[(\frac{l}{2})^{2}}\:+\:h^{2}]}$$

紙鎮的總表面積

$$\mathrm{=\:6\times\:4\:+\:6\sqrt{[(\frac{4}{2})^{2}\:+\:5^{2}]}\:+\:4\sqrt{[(\frac{l}{2})^{2}}\:+\:5^{2}]\:=\:79.63\:cm^{2}}$$

2)假設一塊木頭被雕刻成一個矩形稜錐，其高度、寬度和長度均為 7 釐米。求這塊木頭的側表面積。

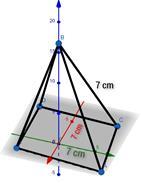
答案 − 矩形稜錐的側表面積

$$\mathrm{=\:l\sqrt{[(\frac{W}{2})^{2}\:+\:h^{2}]}\:+\:w\sqrt{[(\frac{l}{2})^{2}}\:+\:h^{2}]}$$

木頭的側表面積

$$\mathrm{=\:7\sqrt{[(\frac{7}{2})^{2}\:+\:7^{2}]}\:+\:7\sqrt{[(\frac{l}{2})^{2}}\:+\:7^{2}]}$$

$$\mathrm{=\:109.57\:cm^{@}}$$

3)一群 26 個朋友在篝火旁露營。他們在篝火旁搭建了一個大型帳篷，形狀為矩形稜錐，底面積為 300 𝒇𝒕𝟐，垂直高度為 30 英尺。求帳篷的體積。

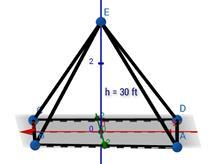
答案 −

$\mathrm{矩形稜錐體積\:=\:\frac{1}{3}\times\:底面積\:\times\:垂直高度}$

$\mathrm{帳篷體積\:=\:\frac{1}{3}\times\:300\times\:30}$

$\mathrm{=\:3000\:ft^{3}}$

4)X 為他的寵物狗建造了一個狗窩，屋頂形狀為矩形稜錐，垂直高度為 20 釐米，底面積為 1800 𝒄𝒎𝟐。求屋頂的體積。

答案 −

矩形稜錐的體積 $\mathrm{=\:\frac{1}{3}\:Bh}$

帳篷的體積 $\mathrm{=\:\frac{1}{3}\times\:1800\times\:20}$

$\mathrm{=\:1.2\times\:10^{5}\:cm^{3}}$

5)假設一個矩形稜錐的體積為 2000 𝒄𝒎𝟑，底面積為 240 𝒄𝒎𝟐。求稜錐的垂直高度。

答案 −

矩形稜錐的體積 $\mathrm{=\:\frac{1}{3}\times\:底面積\times\:垂直高度}$

$\mathrm{2000\:=\:\frac{1}{3}\times\:240\times\:h}$

$\mathrm{600\:=\:24\times\:240\times\:h}$

$\mathrm{100\:=\:4\times\:h}$

$\mathrm{h\:=\:25\:cm}$

6)假設矩形稜錐的高度為 12 釐米，體積為 1800 𝒄𝒎𝟑。求稜錐的底面積。

答案 −

矩形稜錐的體積 $\mathrm{=\:\frac{1}{3}\times\:底面積\:\times\:垂直高度}$

$\mathrm{1800\:=\:\frac{1}{3}\:\times\:B\times\:12}$

$\mathrm{5400\:=\:B\times\:12}$

$\mathrm{1800\:=\:B\times\:4}$

$\mathrm{底面積\:B\:=\:450\:cm^{2}}$

結論

• 具有四個三角形面和一個矩形底面的立體圖形稱為矩形稜錐。

• 矩形稜錐的底面積是其長和寬的乘積。

• 矩形稜錐的總表面積是透過將側表面積和底面積相加來計算的。

• 矩形稜錐的側表面積是透過將所有三角形面的面積相加來計算的。

• 矩形稜錐的體積是透過將其底面積乘以其垂直高度來計算的。

常見問題

1. 什麼是稜錐？請舉一個現實生活中的例子？

透過連線底面和側三角形面形成的立體圖形稱為稜錐。

“稜錐”一詞來源於希臘語，意思是小麥餅，因為希臘人過去常常將埃及的建築物比作尖尖的小麥餅。

埃及吉薩大金字塔是一個合適的例子。

2. 什麼是正方形稜錐？

. 具有四個三角形面和一個正方形底面的立體圖形稱為正方形稜錐。它也被稱為五面體，因為它有五個面。

3. 正方形稜錐和矩形稜錐有什麼區別？

正方形稜錐和矩形稜錐的區別在於底面積，但正方形稜錐可以被稱為矩形稜錐，因為它的表面積和體積與矩形稜錐相同，但反之則不然。

4. 什麼是三角形稜錐？

具有三個三角形面和一個三角形底面的幾何立體圖形稱為三角形稜錐。

5. 如何測量正方形稜錐的體積？

正方形稜錐的體積與矩形稜錐相同，它是透過將底面積和稜錐高度的乘積的三分之一來計算的。