徑向加速度

---

介紹

徑向加速度通常出現在外力作用於物體時，根據牛頓第二定律，加速度是物體速度隨時間的變化率。它是一個向量量，既包含大小也包含方向。

徑向加速度的測量單位是$\mathrm{ms^{-2}}$。簡單來說，徑向加速度指的是物體速度與總時間的特定比例。根據物體的兩種運動型別，徑向加速度也不同。

物體的運動既可以是直線運動也可以是圓周運動。因此，根據運動的不同，物體的加速度也有兩種型別：徑向加速度和切向加速度。

什麼是徑向加速度？

徑向加速度的符號是a，它會隨物體的角速度以及運動方向而不斷變化。物體的運動比例、速度以及運動方向被認為是徑向加速度。它可以定義為速度相對於特定時間的變化率。

徑向加速度被認為是物體指向該物體中心的加速度。這種型別的加速度主要發生在圓周運動中，而物體的運動與物體的半徑有關。

徑向加速度的單位

物體徑向加速度的測量單位有兩種：每秒平方弧度和每秒平方米。

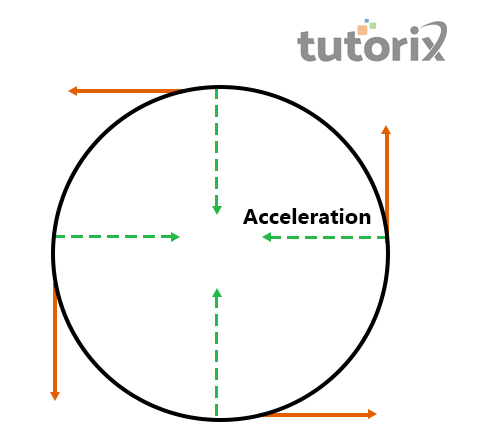
圖1：圓周運動

每秒平方弧度用$\mathrm{\omega s^{-2}}$和$\mathrm{ms^{-2}}$表示。物體的角位移單位是弧度，角速度單位是$\mathrm{弧度/秒}$。$\mathrm{弧度/秒^2}$是角加速度的單位。

徑向加速度：特徵

• 角加速度分為徑向加速度和切向加速度兩種。

• 徑向加速度主要指指向物體中心的物體加速度。

• 當以每秒平方的弧度表示時，徑向加速度可以用$\mathrm{\omega s^{-2}}$單位來測量。

• 徑向加速度也常被稱為向心加速度。

• 切向加速度是指角加速度的主要分量。

• 徑向加速度始終可以表示為瞬時速度，因此通常被稱為一般加速度。

• 它被稱為向心加速度，因為這種型別的加速度主要指向軌跡曲率的瞬時中心。

• 這種型別的運動並非僅定義於圓周運動，而是多種型別的運動。

徑向加速度的分量

徑向加速度取決於一些影響加速度率的分量。角位移是一種可以定義為物體初始位置和最終位置之間角度差的分量。該分量的符號為𝜃，其公式為$\mathrm{\theta = s/r}$。

角位移的單位是弧度。角速度是另一種型別，可以定義為角位移相對於特定時間的變化率。該分量的符號為⍵，其公式為$\mathrm{\omega = d \theta /dt}$ (Brouwer et al. 2021)。角位移的單位是$\mathrm{弧度/秒}$。角加速度是另一種型別，可以定義為角速度相對於特定時間的變化率 (Stone & Courteau, 2019)。

該分量的符號為$\mathrm{\alpha}$，其公式為$\mathrm{\alpha = \frac{d \omega}{dt}}$。角位移的單位是$\mathrm{弧度/秒^2}$。

徑向加速度的公式

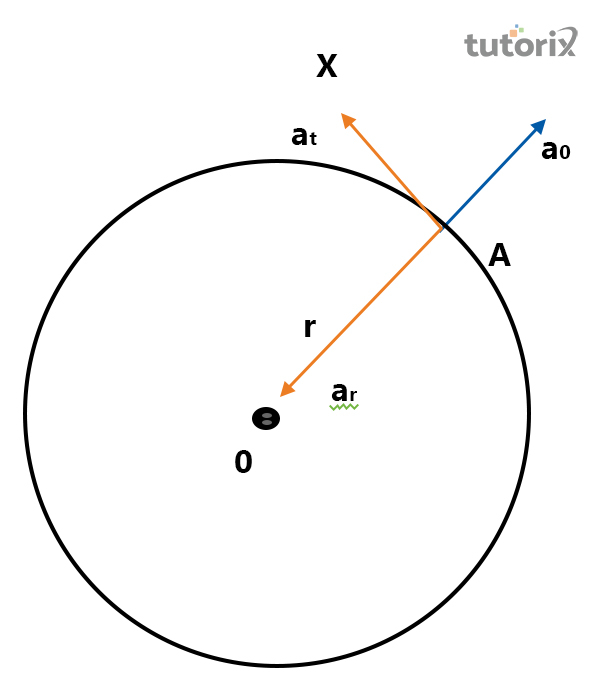
圖2：旋轉運動物體的示意圖

物體A用繩子與另一個物體相連，當它圍繞固定點O旋轉時，看起來像一個圓形半徑。因此，在這種情況下，產生了沿徑向方向的a0加速度。

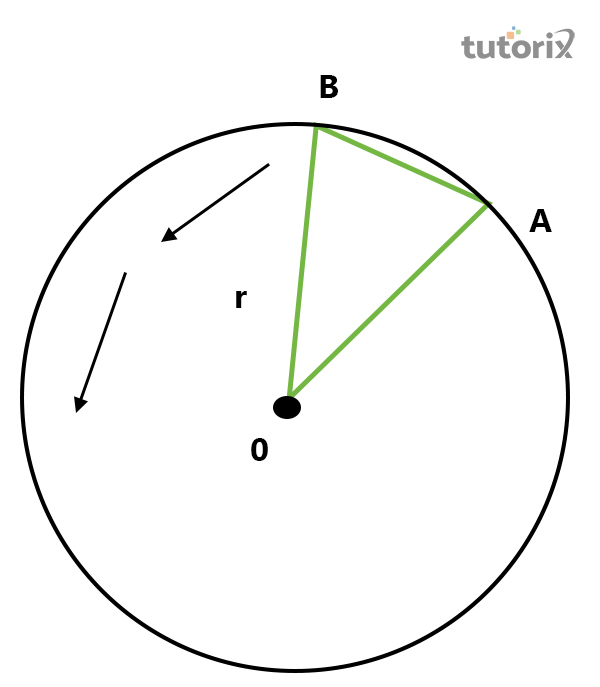
圖3：兩個物體的徑向加速度

對於兩個不同的物體，徑向加速度可以用公式$\mathrm{AB\:=\:v\:\times\:dt}$來測量，其中A和B是兩個物體，它取決於v（表示速度）和dt（表示時間差） (Pradyumna & Desai, 2021)。

如果這兩個物體非常接近，則公式變為$\mathrm{v\:+\:dv\:≈\:dv\:\times\:AB/OA}$，也可以表示為$\mathrm{dv/v\:=\:v^2/r}$。對於切向加速度，公式為$\mathrm{at\:=\:v^2-v1/t}$，其中，at表示切向分量，t表示時間段，$\mathrm{v^2}$或$\mathrm{v^3}$表示從圓周運動中獲得的兩個不同物體的速度結果。

結論

在任何時刻，徑向加速度的大小為$\mathrm{v^2/r}$，其中v代表物體的速度，r是任何時刻曲率的半徑。在圓周運動中，$\mathrm{r}$指半徑，徑向加速度的方向與曲率半徑相同。在勻速圓周運動(UCM)中，切向加速度始終定義為零，因為物體的速度是相同的。在任何型別的直線運動中，徑向加速度始終為零，因為曲率半徑在直線上，指的是無限大。

常見問題

Q1. 加速度和減速度是什麼？

加速度和減速度都是物體速度的變化。這兩個粒子的速率取決於時間。

Q2. 角運動有哪些型別？

角運動有兩種不同的型別：徑向加速度和切向加速度。這兩種型別都取決於速度和時間。

Q.3 什麼是角速度？

角位移的時間變化率稱為角速度。其公式為$\mathrm{(\omega) = (\delta \theta /\delta t)}$。

Q4. 加速度有哪些型別？

線加速度和圓加速度是兩種型別的加速度。沿曲線軌跡運動的物體的物體包含非零徑向加速度。