Python 語言第 n 個 Catalan 數

在本文中，我們將學習如何計算第 n 個 Catalan 數。

Catalan 數是自然數序列，由遞迴公式定義：−

$$C_{0}= 1\:and\:C_{n+1}=\displaystyle\sum\limits_{i=0}^n C_{i}C_{n-i} for \:n\geq0;$$

對於 n = 0, 1, 2, 3, …，前幾個 Catalan 數為1, 1, 2, 5, 14, 42, 132,429,...................

Catalan 數既可以透過遞迴獲得，也可以透過動態規劃獲得。下面讓我們看看它們的實現方式。

方法 1： 遞迴方法

示例

 演示

# A recursive solution
def catalan(n):
   #negative value
   if n <=1 :
      return 1
   # Catalan(n) = catalan(i)*catalan(n-i-1)
   res = 0
   for i in range(n):
      res += catalan(i) * catalan(n-i-1)
   return res
# main
for i in range(6):
   print (catalan(i))

輸出

1
1
2
5
14
42

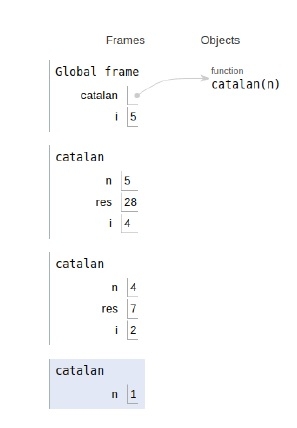
所有變數和遞迴呼叫的範圍如下所示。

方法 2：動態規劃方法

示例

 演示

# using dynamic programming
def catalan(n):
   if (n == 0 or n == 1):
      return 1
   # divide table
   catalan = [0 for i in range(n + 1)]
   # Initialization
   catalan[0] = 1
   catalan[1] = 1
   # recursion
   for i in range(2, n + 1):
      catalan[i] = 0
      for j in range(i):
         catalan[i] = catalan[i] + catalan[j] * catalan[i-j-1]
   return catalan[n]
# main
for i in range (6):
   print (catalan(i),end=" ")

輸出

1
1
2
5
14
42

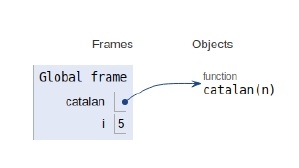
所有變數和遞迴呼叫的範圍如下所示。

結論

在本文中，我們瞭解了生成第 n 個 Catalan 數的方法。

Pavitra

更新於： 2019 年 9 月 11 日

341 次瀏覽

開啟您的職業生涯

透過完成課程獲得認證

開始