資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究Python程式：查詢圖中的關鍵邊和偽關鍵邊
假設我們得到一個包含n個頂點的圖，編號從0到n-1。圖是無向圖，每條邊都有權重。因此，給定圖，我們必須找到圖的最小生成樹中的關鍵邊和偽關鍵邊。如果刪除該邊會導致最小生成樹的權重增加，則該邊稱為關鍵邊。偽關鍵邊是可以出現在所有圖的最小生成樹中，但並非全部出現的邊。我們根據給定的圖作為輸入找到邊的索引。
因此，如果輸入如下所示：
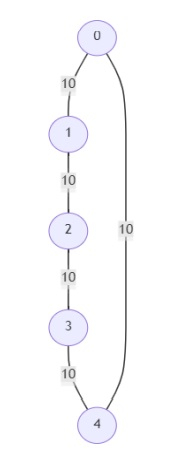
且頂點數為5，則輸出將為[[], [0, 1, 2, 3, 4]]。給定圖中沒有關鍵邊，所有邊都是偽關鍵邊。由於所有邊的權重都相同，因此圖中的任意3條邊將構成一個最小生成樹。
要解決此問題，我們將遵循以下步驟：
定義一個函式find_mst()。它將接收num_vertices、graph、init（預設為null）、exl（預設為null）作為引數。
定義一個輔助函式visit()。它將接收u作為引數。
k[u] := True
對於graph[u]中的每個v、w（一個空列表），執行以下操作：
如果exl不為空，並且u在exl中，且v在exl中，則：
跳過本次迭代。
如果k[v]不為True，則：
將三元組(w,u,v)推入堆tmp。
res := 0
k := 一個大小為num_arrays的新列表，所有元素都為False。
tmp := 一個新的堆。
如果init不為null，則：
u := init
v := init
w := init
res := res + w
k[u] := True
k[v] := True
visit(u) 或 visit(v)
否則，
visit(0)
當tmp不為空時，執行以下操作：
w := 從堆tmp中彈出最小元素。
u := 從堆tmp中彈出最小元素。
v := 從堆tmp中彈出最小元素。
如果k[u]和k[v]都不為零，則：
跳過本次迭代。
res := res + w
如果k[u]不為True，則：
visit(u)
如果k[v]不為True，則：
visit(v)
如果所有k都為True，則返回res，否則返回無窮大。
在主方法中，執行以下操作：
graph := 給定的圖。
temp := find_mst(num_vertices, graph)。
c_edge := 一個新列表。
p_edge := 一個新列表。
對於範圍0到edges的大小，執行以下操作：
如果find_mst(num_vertices, graph, exl = edges[i, index 2 to end]) > temp，則：
將i插入c_edge的末尾。
否則，如果find_mst(num_vertices, graph, init = edges[i])等於temp，則：
將i插入p_edge的末尾。
返回[c_edge, p_edge]。
示例
讓我們看一下下面的實現，以便更好地理解。
from heapq import heappop, heappush
def solve(num_vertices, edges):
graph = dict()
for u, v, w in edges:
graph.setdefault(u, []).append((v, w))
graph.setdefault(v, []).append((u, w))
temp = find_mst(num_vertices, graph)
c_edge, p_edge = [], []
for i in range(len(edges)):
if find_mst(num_vertices, graph, exl = edges[i][:2]) > temp:
c_edge.append(i)
elif find_mst(num_vertices, graph, init = edges[i]) == temp:
p_edge.append(i)
return [c_edge, p_edge]
def find_mst(num_vertices, graph, init = None, exl = None):
def visit(u):
k[u] = True
for v, w in graph.get(u, []):
if exl and u in exl and v in exl:
continue
if not k[v]:
heappush(tmp, (w, u, v))
res = 0
k = [False] * num_vertices
tmp = []
if init:
u, v, w = init
res += w
k[u] = k[v] = True
visit(u) or visit(v)
else:
visit(0)
while tmp:
w, u, v = heappop(tmp)
if k[u] and k[v]: continue
res += w
if not k[u]:
visit(u)
if not k[v]:
visit(v)
return res if all(k) else inf
print(solve(5, [[0,1,10],[1,2,10],[2,3,10],[3,4,10],[4,0,10]]))輸入
5, [[0,1,10],[1,2,10],[2,3,10],[3,4,10],[4,0,10]]
輸出
[[], [0, 1, 2, 3, 4]]
561 次檢視
