資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學Python程式：判斷圖是否可被所有人遍歷
假設我們有一個包含n個頂點（編號為0到n-1）的圖。該圖是無向圖，每條邊都有權重。圖的權重可以是三種類型，每種權重代表一項特定任務。有兩個人可以遍歷該圖，分別是Jack和Casey。如果一條邊的權重為1，Jack可以遍歷該圖；如果權重為2，Casey可以遍歷該圖；如果權重為3，Jack和Casey都可以遍歷該圖。我們必須移除必要的邊以使圖對Jack和Casey都可遍歷。我們需要返回要移除的邊的數量，如果圖無法使其對兩者都可遍歷，則返回-1。
例如，輸入：
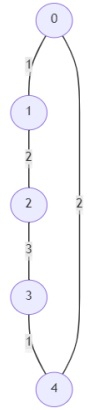
n = 5；則輸出為-1
該圖無法透過移除邊使其對兩者都可遍歷。因此，答案是-1。
為了解決這個問題，我們將遵循以下步驟：
定義一個函式`find()`。它將接收`val`作為引數。
如果`val`不等於`root[val]`，則
`root[val] := find(root[val])`
返回`root[val]`
定義一個函式`union()`。它將接收`val1`，`val2`作為引數。
`val1 := find(val1)`
`val2 := find(val2)`
如果`val1`等於`val2`，則
返回0
`root[val1] := val2`
返回1
`res := 0`
`edge1 := 0`
`edge2 := 0`
`root :=` 從0到n+1的新列表
對於每條邊(u, v)及其權重w在e中，執行：
如果u等於3，則
如果`union(v, w)`不為零，則
`edge1 := edge1 + 1`
`edge2 := edge2 + 1`
否則，
`res := res + 1`
`root0 := root[0...n]`
對於每條邊(u, v)及其權重w在e中，執行：
如果u等於1，則
如果`union(v, w)`不為零，則
`edge1 := edge1 + 1`
否則，
`res := res + 1`
`root := root0`
對於每條邊(u, v)及其權重w在e中，執行：
如果u等於2，則
如果`union(v, w)`不為零，則
`edge2 := edge2 + 1`
否則，
`res := res + 1`
如果`edge1`等於`edge2`且等於`n - 1`，則返回`res`
否則，返回-1
示例
讓我們看看下面的實現，以便更好地理解。
def solve(n, e):
def find(val):
if val != root[val]:
root[val] = find(root[val])
return root[val]
def union(val1, val2):
val1, val2 = find(val1), find(val2)
if val1 == val2: return 0
root[val1] = val2
return 1
res = edge1 = edge2 = 0
root = list(range(n + 1))
for u, v, w in e:
if u == 3:
if union(v, w):
edge1 += 1
edge2 += 1
else:
res += 1
root0 = root[:]
for u, v, w in e:
if u == 1:
if union(v, w):
edge1 += 1
else:
res += 1
root = root0
for u, v, w in e:
if u == 2:
if union(v, w):
edge2 += 1
else:
res += 1
return res if edge1 == edge2 == n - 1 else -1
print(solve(5, [(0,1,1),(1,2,2),(2,3,3),(3,4,1),(4,0,2)]))輸入
Input: 5, [(0,1,1),(1,2,2),(2,3,3),(3,4,1),(4,0,2)]
輸出
-1
瀏覽量：133
