資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學Python程式檢查圖中是否存在任何公共可達節點
假設我們有一個有向圖的邊列表，有n個節點，節點名稱為0到n-1。我們還有兩個整數值a和b。我們必須檢查是否存在任何節點c，使得我們可以從c到a，也可以從c到b。
因此，如果輸入如下所示：
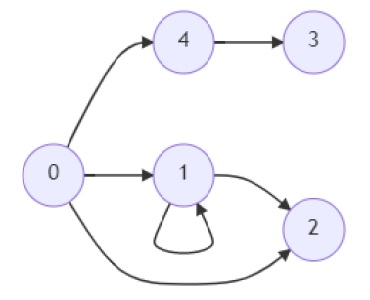
並且a = 2，b = 3，則輸出為True，因為這裡c = 0，所以我們有從0到2和從0到3的路徑。
為了解決這個問題，我們將遵循以下步驟：
- 定義一個函式DFS()。這將接受圖、節點和已訪問節點。
- 如果節點未被訪問，則
- 標記節點為已訪問
- 對於graph[node]中的每個x，執行
- DFS(graph, x, visited)
- 在主方法中，執行以下操作：
- graph := 從edge_list生成鄰接表
- visited_a, visited_b := 兩個空集合
- DFS(graph, a, visited_a)
- DFS(graph, b, visited_b)
- ans := 從visited_b和visited_a的交集生成一個新列表
- 如果ans不為空，則
- 返回True
- 返回False
示例
讓我們看看下面的實現以更好地理解：
def edge_list_to_graph(edges): s = set() for x, y in edges: s.add(x) s.add(y) s = len(list(s)) graph = [[] for x in range(s)] for x, y in edges: graph[y].append(x) return graph def DFS(graph, node, visited): if node not in visited: visited.add(node) for x in graph[node]: DFS(graph, x, visited) def solve(edges, a, b): graph = edge_list_to_graph(edges) visited_a, visited_b = set(), set() DFS(graph, a, visited_a) DFS(graph, b, visited_b) ans = list(visited_a.intersection(visited_b)) if ans: return True return False ed_list = [(0, 4),(4, 3),(1, 2),(0, 1),(0, 2),(1, 1)] a = 2 b = 3 print(solve(ed_list, a, b))
輸入
[(0, 4),(4, 3),(1, 2),(0, 1),(0, 2),(1, 1)], 2, 3
輸出
True
更新於：2021年10月16日
290 次瀏覽
廣告