資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝設計
法學檢查給定兩個三角形相似度的程式
在這個問題中，我們將學習如何檢查給定兩個三角形的相似性，從程式設計師的角度來看，這在現實世界中有很多應用案例。
為了構建和管理物體的二維和三維模型，使用 CAD 系統，而一個關鍵功能是比較兩個三角形的能力。
例如，從事設計和施工的工程師可能需要確保建築物的基礎測量與藍圖相符。工程師可以使用具有內建功能來檢查兩個三角形相似性的 CAD 工具，快速評估地基的角和邊是否與佈局匹配。這有助於確保建築物的結構穩定性和安全性。
此外，三維列印技術透過 CAD 軟體生成物體的三維模型。在這種情況下，相似性檢查有助於確保模型列印精確並按所需比例進行。對於複雜的模型，這至關重要，因為手動驗證相似性可能既繁瑣又容易出錯。
在機器人技術領域，程式設計師可以使用相似性檢查工具來確保機器人運動的精度。檢查兩個三角形的相似性有助於確保機器人手臂（通常具有多個關節）執行的複雜運動精確且一致。
解釋
現在讓我們瞭解計算三角形相似性中涉及的一些數學知識。
如果兩個三角形具有以下特徵，則它們相似：
兩個三角形的角度相等。
三角形的對應邊具有相同的比例。
有三種方法可以確定兩個三角形是否相似：SSS、SAS 和 AA。讓我們簡要討論每個定理。
SSS（邊邊邊）準則
在給定的兩個三角形中，如果三對邊的比例相同，則這兩個三角形相似。
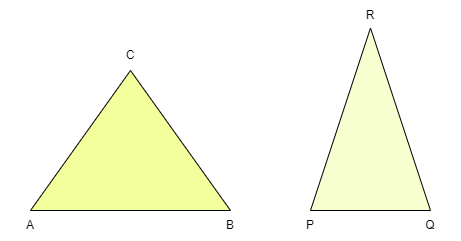
讓我們考慮上面給出的兩個三角形。如果三對邊的比例相等，即 AC/PR = AB/PQ = CB/RQ，則上述兩個三角形可以透過 SSS 準則相似。
SAS（邊角邊）準則
在給定的兩個三角形中，如果兩對邊的比例相同，並且這兩個邊之間的角度在兩個三角形中都相同，則這兩個三角形相似。
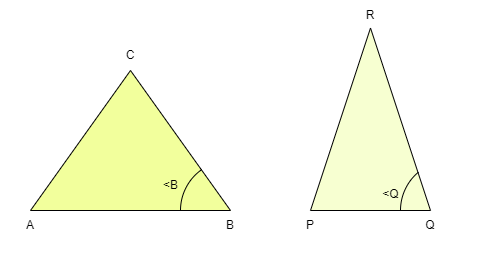
如果我們以上面的三角形為例，那麼如果 AB/PQ = BC/QR 且∠B = ∠Q，則這兩個三角形透過 SAS 準則相似。
AA（角角）準則
在給定的兩個三角形中，如果兩個三角形的任意兩個角相等，則這兩個三角形相似。
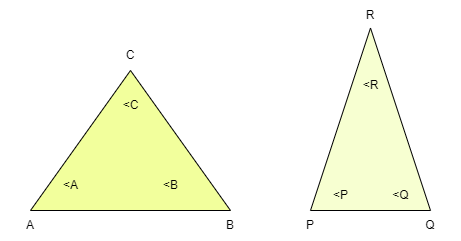
如果我們以上面的三角形為例，那麼如果∠A =∠P 且∠B =∠Q，或者∠A =∠P 且∠C =∠R，或者存在任何此類組合，則這兩個三角形透過 AA 準則相似。
通常，我們得到三角形三個點的座標，然後我們需要檢查相似性。在這種情況下，我們將使用此公式計算距離。
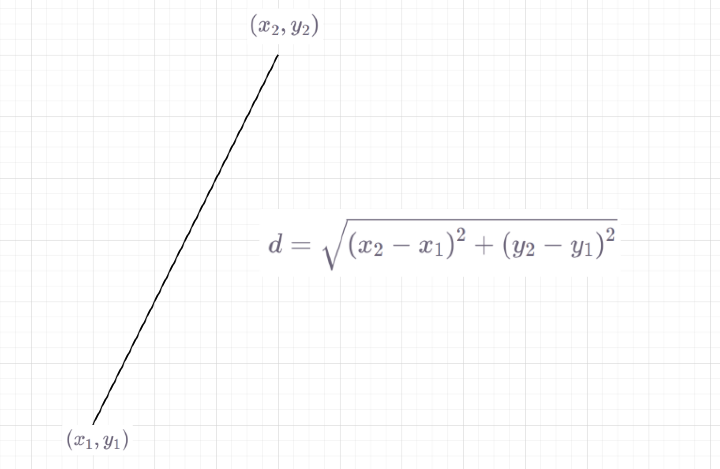
當提供座標時，用於檢查給定兩個三角形相似度的程式。
方法
讓我們將整個程式解碼為逐步演算法
將兩個三角形三個點的座標作為輸入。
使用上面討論的公式計算座標之間的長度，即 distance= Math.sqrt(Math.pow(y2-y1,2)+Math.pow(x2-x1,2))
計算兩個三角形所有邊的長度後，計算所有對的比例。
接下來，檢查所有三個比例是否相同，如果相同，則列印三角形相似，否則列印三角形不相似。
現在，我們將編寫實現上述演算法的程式碼
示例
當提供座標時，用於檢查給定兩個三角形相似性的 C++ 程式。
#include <iostream>
#include <cmath>
using namespace std;
int main() {
double x1 = 0, y1 = 0, x2 = 3, y2 = 0, x3 = 0, y3 = 4; //coordinates of first triangle (x1, y1), (x2, y2), (x3, y3)
double p1 = 0, q1 = 0, p2 = 6, q2 = 0, p3 = 0, q3 = 8; //coordinates of second triangle (p1, q1), (p2, q2), (p3, q3)
// calculate the distance between the coordinates of the first triangle
double dist1 = sqrt(pow((x2 - x1), 2) + pow((y2 - y1), 2));
double dist2 = sqrt(pow((x3 - x2), 2) + pow((y3 - y2), 2));
double dist3 = sqrt(pow((x1 - x3), 2) + pow((y1 - y3), 2));
// calculate the distance between the coordinates of the second triangle
double dist4 = sqrt(pow((p2 - p1), 2) + pow((q2 - q1), 2));
double dist5 = sqrt(pow((p3 - p2), 2) + pow((q3 - q2), 2));
double dist6 = sqrt(pow((p1 - p3), 2) + pow((q1 - q3), 2));
// calculate the ratio of the length of the triangle
double ratio1 = dist1/dist4;
double ratio2 = dist2/dist5;
double ratio3 = dist3/dist6;
// check if the ratio of all three pairs of sides of the triangle are same, we are using SSS criteria
if ((ratio1 == ratio2) && (ratio2 == ratio3)) {
cout << "The two triangles are similar." << endl;
} else {
cout << "The two triangles are not similar." << endl;
}
return 0;
}
輸出
The two triangles are similar.
複雜度
時間複雜度：O(1)，因為這段程式碼執行的計算次數是固定的，與輸入的大小無關。
空間複雜度：O(1)，因為這段程式碼使用固定數量的變數來儲存輸入值和結果，與輸入的大小無關。
當提供座標時，用於檢查給定兩個三角形相似度的程式。
方法
讓我們將整個程式解碼為逐步演算法
將三角形的角度作為輸入。
比較角度以檢查三角形的任意兩個角度是否相同，這裡我們使用 AA 準則。
如果任意兩個角度相同，則列印三角形相似，否則列印三角形不相似。
現在，我們將編寫實現上述演算法的程式碼。
示例
當提供角度時，用於檢查給定兩個三角形相似性的 C++ 程式。
#include <iostream>
using namespace std;
bool check_aa(int a1,int a2,int a3,int a4,int a5,int a6){
if((a1==a4 || a1==a5 || a1==a6) && (a2==a4 || a2==a5 || a2==a6))
return true;
else
return false;
}
int main(){
// Input: the angles of the triangles
double a1 = 30, a2 = 60, a3 = 90; //angles of triangle A
double a4 = 60, a5 = 90, a6 = 30; //angles of triangle B
bool similar= check_aa(a1,a2,a3,a4,a5,a6);
if (similar)
cout << "The two triangles are similar." << endl;
else
cout << "The two triangles are not similar." << endl;
}
輸出
The two triangles are similar.
複雜度
時間複雜度：O(1)，因為這段程式碼執行的計算次數是固定的，與輸入的大小無關。
空間複雜度：O(1)，因為這段程式碼使用固定數量的變數來儲存輸入值和結果，與輸入的大小無關。
結論
在本文中，我們嘗試根據兩種情況解釋檢查兩個三角形相似性的方法，一種是提供邊作為輸入，另一種是提供角作為輸入。我希望本文能幫助您更好地學習這個概念。
391 次檢視
