資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究C++ 中二維列印二叉樹
在這個問題中，我們給定一棵二叉樹，需要將其列印到二維平面上。
二叉樹是一種特殊的樹，其每個節點最多有兩個子節點。因此，每個節點要麼是葉子節點，要麼有一個或兩個子節點。
示例：
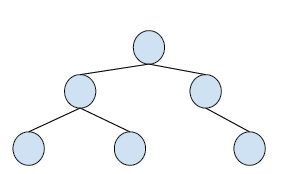
讓我們舉一個例子來更好地理解這個主題：
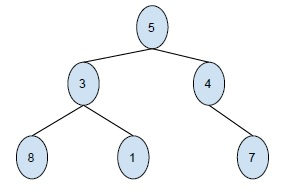
輸出 -
7 4 5 1 3 8
正如我們在示例中看到的，樹的節點以水平方式列印到二維輸出螢幕上。
在這裡，我們將樹旋轉了 90 度。
讓我們看看新的水平樹由什麼組成：
樹的資料結構以水平方式儲存，包括
根節點位於水平檢視中第一個位置，起始行下方 n 行。即根節點將位於第 n 行的開頭。
樹的新層位於 n+i 行和 n-i 行。並且距離行首 i 個製表符空格。
樹的最右邊的葉子節點列印在第一行。而樹的最左邊的節點列印在最後一行。
示例
讓我們根據此邏輯建立一個程式：
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
#define COUNT 10
class Node{
public:
int data;
Node* left, *right;
Node(int data){
this->data = data;
this->left = NULL;
this->right = NULL;
}
};
void printTree(Node *root, int space){
if (root == NULL)
return;
space += COUNT;
printTree(root->right, space);
for (int i = COUNT; i < space; i++)
cout<<"\t";
cout<<root->data<<"\n";
printTree(root->left, space);
}
int main(){
Node *root = new Node(43);
root->left = new Node(25);
root->right = new Node(67);
root->left->left = new Node(14);
root->left->right = new Node(51);
root->right->left = new Node(26);
root->right->right = new Node(97);
root->left->left->left = new Node(81);
root->left->left->right = new Node(49);
root->left->right->left = new Node(07);
root->left->right->right = new Node(31);
root->right->left->left = new Node(29);
root->right->left->right = new Node(13);
root->right->right->left = new Node(59);
root->right->right->right = new Node(16);
printTree(root, 0);
return 0;
}輸出
16 97 59 67 13 26 29 43 31 51 7 25 49 14 81
更新於：2020-01-03
899 次檢視
廣告