資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法學研究用 C++ 列印二叉樹中具有 K 個葉子節點的所有節點
在這個問題中，我們給定一棵二叉樹和一個整數 K，我們必須列印二叉樹中所有在其子樹中具有 K 個葉子節點的節點。
二叉樹是一種特殊的樹，其每個節點最多有兩個子節點（一個/兩個/零個）。
葉子節點是二叉樹末端的節點。
讓我們來看一個例子來理解這個問題：
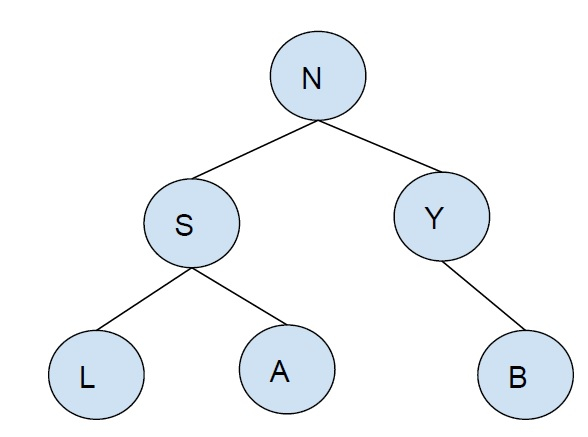
K = 2
輸出： {S}
為了解決這個問題，我們將對樹進行遍歷（後序遍歷）。現在，我們將檢視每個左子樹和右子樹，如果葉子節點之和為 K，則列印當前節點；否則遞迴呼叫子樹的葉子節點計數。
此解決方案基於遍歷，因此複雜度將與樹的大小成正比。時間複雜度： O(n)
示例
實現上述方法的程式
#include<bits/stdc++.h>
using namespace std;
struct Node{
char data ;
struct Node * left, * right ;
};
struct Node * insertNode(char data){
struct Node * node = new Node;
node->data = data;
node->left = node->right = NULL;
return (node);
}
int nodeWithKLeave(struct Node *ptr,int k){
if (ptr == NULL)
return 0;
if (ptr->left == NULL && ptr->right == NULL)
return 1;
int total = nodeWithKLeave(ptr->left, k) + nodeWithKLeave(ptr->right, k);
if (k == total)
cout<<ptr->data<<" ";
return total;
}
int main() {
struct Node *root = insertNode('A');
root->left = insertNode('B');
root->right = insertNode('K');
root->left->left = insertNode('N');
root->left->right = insertNode('S');
root->left->left->left = insertNode('X');
root->left->left->right = insertNode('H');
root->right->right = insertNode('E');
root->right->left = insertNode('T');
root->right->left->left = insertNode('O');
root->right->left->right = insertNode('P');
int K = 2;
cout<<"Nodes with "<<K<<" leaves is :\n";
nodeWithKLeave(root, K);
return 0;
}輸出
Nodes with 2 leaves are: N T
更新於：2020年1月22日
125 次瀏覽
廣告