資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究在 C++ 中列印給定節點距離 K 的所有節點
在這個問題中，我們給定一棵二叉樹、一個目標節點和一個整數 K。我們必須列印樹中所有與目標節點距離為 K 的節點。
二叉樹是一種特殊的樹，其每個節點最多有兩個子節點（一個/兩個/零個）。
讓我們舉一個例子來理解這個問題
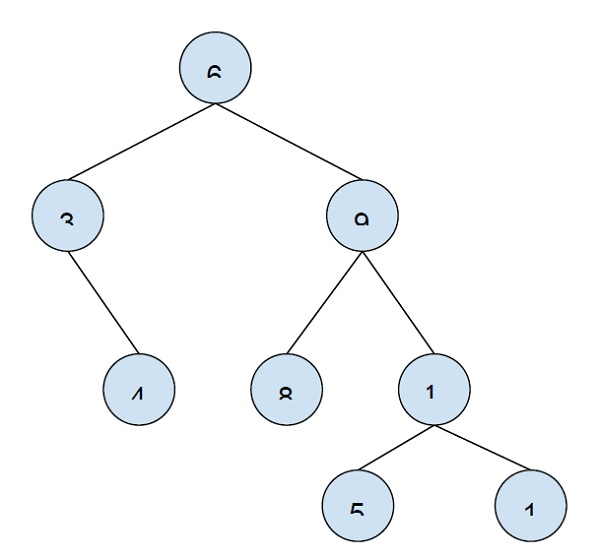
K = 2
目標節點：9
輸出 -
5 1 3.
解釋 -
節點的距離可以向上、向下或在同一層級上計算。因此，我們將相應地返回節點。
為了解決這個問題，我們必須理解與目標節點距離為 K 的節點的型別。
從上面的例子中，我們可以看到距離為 k 的節點可能位於目標節點的子樹中（5 和 1），或者位於目標節點的祖先節點（3）的子樹中的任何位置。
現在，解決第一種情況的方法是遍歷目標節點的子樹，並檢查節點與目標節點的距離是否為 K。如果是，則列印該節點。
對於第二種情況，我們必須檢查祖先節點以及這些祖先節點的子樹，以找到目標節點，並列印所有與它距離為 K 的節點。
下面的程式將展示我們解決方案的實現 -
示例
#include <iostream>
using namespace std;
struct node {
int data;
struct node *left, *right;
};
void printSubtreeNodes(node *root, int k) {
if (root == NULL || k < 0) return;
if (k==0){
cout<<root->data<<"\t";
return;
}
printSubtreeNodes(root->left, k-1);
printSubtreeNodes(root->right, k-1);
}
int printKNodes(node* root, node* target , int k){
if (root == NULL) return -1;
if (root == target){
printSubtreeNodes(root, k);
return 0;
}
int dl = printKNodes(root->left, target, k);
if (dl != -1){
if (dl + 1 == k)
cout<<root->data<<"\t";
else
printSubtreeNodes(root->right, k-dl-2);
return 1 + dl;
}
int dr = printKNodes(root->right, target, k);
if (dr != -1){
if (dr + 1 == k)
cout << root->data << endl;
else
printSubtreeNodes(root->left, k-dr-2);
return 1 + dr;
}
return -1;
}
node *insertNode(int data){
node *temp = new node;
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
int main(){
node * root = insertNode(6);
root->left = insertNode(3);
root->right = insertNode(9);
root->left->right = insertNode(4);
root->right->left = insertNode(8);
root->right->right = insertNode(10);
root->right->right->left = insertNode(5);
root->right->right->right = insertNode(1);
node * target = root->right;
int K = 2;
cout<<"Nodes at distance "<<K<<" from the target node are :\n";
printKNodes(root, target, K);
return 0;
}輸出
Nodes at distance 2 from the target n tode are − 5 1 3
更新於：2020年1月22日
417 次檢視
廣告