資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會研究
時尚研究
法律研究使用 DFS 以 C++ 語言列印一個 n 叉樹的所有葉節點
在這個題目中，我們給定一個二維陣列，其中包含 n 叉樹的邊，邊定義了 n 叉樹的邊緣。我們必須列印所建立的 a 叉樹的所有葉節點。
n 叉樹是一個有 n 個子節點的樹，即一個節點可以有 1、2、...n 個子節點。
我們透過一個例子來理解題目 -
Input: edge[][] = {{5,8}, {5,6}, {8,1}, {8,4}, {6,7}}
Output: 1 4 7說明 -讓我們使用邊陣列建立一個樹 -
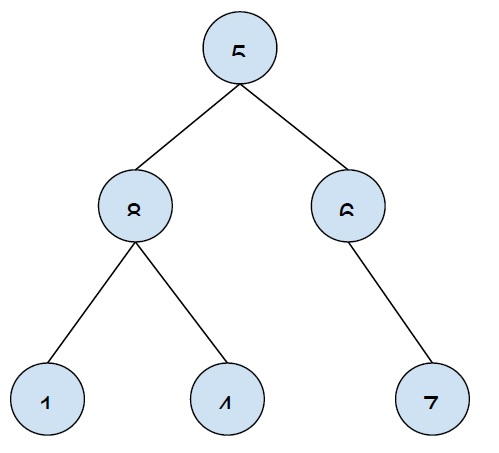
這棵樹的葉節點是 1、4、7。
要解決這個問題，我們將使用 DFS 遍歷這棵樹（它將找到每個子樹的葉節點）。同時，陣列的已訪問節點被打上標記。如果節點有子節點（如果不是葉節點），我們將標記該值並列印沒有子節點的節點。
示例
這個程式展示了我們解決方案的實現 -
#include <bits/stdc++.h>
using namespace std;
void DFS(list<int> t[], int node, int parent) {
int flag = 0;
for (auto ir : t[node]) {
if (ir != parent) {
flag = 1;
DFS(t, ir, node);
}
}
if (flag == 0)
cout<<node<<"\t";
}
int main() {
list<int> t[1005];
pair<int, int> edges[] = {
{ 1, 2 },
{ 1, 3 },
{ 2, 4 },
{ 3, 5 },
{ 3, 6 },
{ 3, 7 },
{ 6, 8 }
};
int cnt = sizeof(edges) / sizeof(edges[0]);
int node = cnt + 1;
for (int i = 0; i < cnt; i++) {
t[edges[i].first].push_back(edges[i].second);
t[edges[i].second].push_back(edges[i].first);
}
cout<<"Leaf nodes of the tree are:\n";
DFS(t, 1, 0);
return 0;
}輸出
Leaf nodes of the tree are − 4 5 8 7
更新於: 2020-01-22
490 次瀏覽
廣告