週期函式

---

簡介

為了理解波和訊號的研究，使用了週期表。在物理學中，人們觀察到運動負責在特定時間間隔內返回到相同的值。基於這些特定概念，所有型別的週期運動都被稱為週期函式。專注於這些概念，本教程包含了與週期函式相關的資訊，以及它的性質和公式。

什麼是週期函式？

在過程中，基於固定的時間間隔，重複發生的運動通常稱為週期函式。因此，週期函式可以定義為在每個時間單位內恢復到相似值的特定函式（Zafar 等人，2020）。週期函式的週期運動可以分為兩種不同的型別：振盪運動和簡諧運動。

圖 1：週期函式

然而，振盪運動和週期運動之間存在差異，因為人們觀察到週期運動與任何在一段時間內表現出重複的運動相關。（Analyzemath.com，2022）。

另一方面，振盪運動指的是在兩個狀態或圍繞平衡點執行的運動，如下面的圖所示。

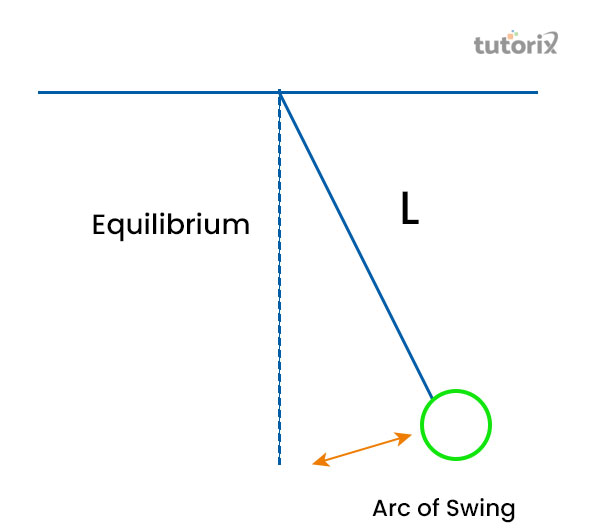
圖 2：振盪運動

為了理解這兩個不同的概念，需要將擺的運動納入考慮。擺有一個特定的平衡位置，它會形成一個擺動的弧線，運動使擺來回運動。

週期函式的性質

為了更深入地理解這個概念，需要了解週期函式的性質。

• 第一個需要了解的屬性是週期“函式的圖形是”對稱的”，它沿水平軸重複自身（Galileospendulum.org，2022）。
• 接下來，“週期函式的定義域包含”所有實數值，並且“週期”運動的“值域”在“固定區間”內識別。週期，即物體在一致的運動中重複自身的時間，在整個函式的值域中被認為是一致的。

重要的週期函式

“尤拉公式”

以數學家“萊昂哈德·尤拉”的名字命名，它被認為是一個“數學公式”，有助於建立指數函式和三角函式之間的關係（Galileospendulum.org，2022）。這個公式通常用於表示“具有 2π/k 週期的特定週期”函式。

“雅可比橢圓函式”

圖 3：雅可比橢圓函式

這種函式的圖形形狀是橢圓形而不是圓形，用於求解“三角函式”（Semanticscholar.org，2022）。透過“涉及振幅和速度這兩個變數”，產生了橢圓形。在描述擺的運動時，觀察到使用了這些型別的函式。

傅立葉級數

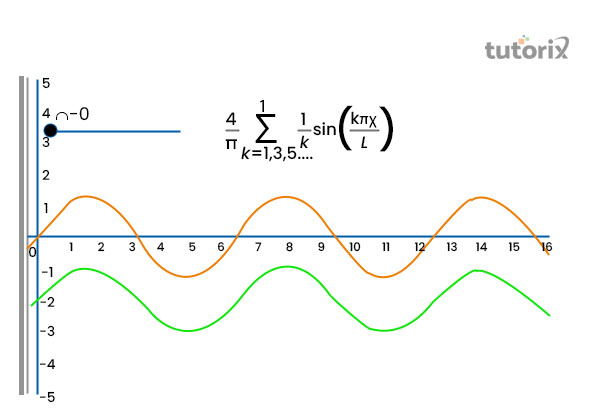
圖 4：傅立葉級數

不同“週期波函式級數”的疊加導致了最強週期函式的形成，通常稱為傅立葉級數。這種函式的構成通常由正弦和餘弦函式進行。在熱波、量子力學和振動分析的表示中，觀察到傅立葉級數的應用。

週期函式的公式

為了計算週期函式，使用的特定公式是 f(x + P) = f(x)。在這個公式中，f 用於指代週期函式，其中此元件被認為是一個非零常數，由 P 表示 x 的值。另一方面，如果函式 h 擴充套件到所有 R，則方程將變成 h(t + 2)= h(t)（Geogebra.org，2022）。這表明方程的值取決於某些方面，例如 P 必須是實數。兩個波之間經過的時間需要是恆定的。

週期函式的例子

為了找到 Tan3x + Sin5x/2 的週期，將考慮 Tanx 的週期為 π。因此，Tanx 的週期將等價於 π/3。相反，Sinx 的週期是 2π。基於此概念化，Sin5x/2 的值將等價於 2π/5/2（Analyzemath.com，2022）。

此公式將等於 4π/5 的值。根據上述找到的方程，“週期函式 f(x)= tan3x + Sin5x/2 的計算”如下

$$\mathrm{f(x)=\frac{π與4π的最小公倍數}{3與5的最大公約數}}$$

此特定計算的值將為 4π/1，這將等價於 4π。因此，在提供的方程 Tan3x +Sin5x/2 中找到的週期的最終值為 4π。

結論

本教程闡明瞭與週期函式相關的解釋，以及“週期函式”公式的表示。人們已經看到，如果觀察到實數的存在，則函式“f(x)”通常被認為是“週期函式”。“週期函式的週期”是指重複間隔的長度。除此之外，還說明了幾個屬性，包括週期函式需要表示實數，並且圖形需要是對稱的。

常見問題

Q1.週期函式中的週期是什麼？

眾所周知，週期函式必須包含物體的重複模式。重複模式具有與時間週期一致的圖形表示，該時間週期表示每次迴圈之間相同型別的間隔長度。這種重複間隔的長度在週期函式中稱為週期。

Q2.如何識別函式為週期函式？

在這種情況下，識別函式中觀察到的重複的特定範圍以及正數值的存在有助於確定方程為週期函式。根據提到的週期函式公式 f(x + T) = f(x)，需要確定 T 的值為最小值。

Q3.週期函式的相移是什麼？

值的相移通常由在規則間隔內觀察到的值的改變來確定。相移的例項包括正值。

Q4.週期函式的值域是什麼？

人們已經觀察到，週期函式包括受限值的範圍。值域通常由一系列正值表示。這組值受重複的影響，以在值中實現不同的定義域。週期函式的值域是指類似的較高值。

參考文獻

期刊

Zafar, A., Raheel, M., Ali, K. K., & Razzaq, W. (2020). 基於雅可比橢圓函式的新哈密頓振幅方程的光學孤子解。歐洲物理雜誌 Plus，135(8)，1-17。檢索自：https://www.researchgate.net

網站

Analyzemath.com，(2022)。關於週期函式。檢索自：https://www.analyzemath.com/function/periodic.html [檢索日期：2022 年 6 月 7 日]

Galileospendulum.org。 (2022)。關於物理量子：擺的擺動。檢索自：https://galileospendulum.org/2011/05/24/physics-quanta-the-pendulums-swing/ [檢索日期：2022年6月7日]

Geogebra.org， (2022)。關於傅立葉級數。檢索自：https://www.geogebra.org/m/eRJ6ygyF [檢索日期：2022年6月7日]

Semanticscholar.org， (2022)。關於雅可比橢圓函式和環上珠子問題的完整解。檢索自：https://www.semanticscholar.org/paper/Jacobi-elliptic-functions-and-the-complete-solution-Baker-Bill/a4e6feff2f92b68b61bd8c06a4c246ecc8da19f3 [檢索日期：2022年6月7日]