給出\( 2 x+9=0 \)作為方程的幾何表示
(i) 單變數
(ii) 雙變數。

待辦事項

我們必須寫出$2x+9=0$作為方程的幾何表示

(i) 單變數，以及

(ii) 雙變數。

解答

(i) 我們知道：

要繪製單變數線性方程的圖形，我們只需要一個解。

已知：

$2x+9=0$

這意味著：

$2x=-9$

$x=\frac{-9}{2}$

$x=-4.5$

因此：

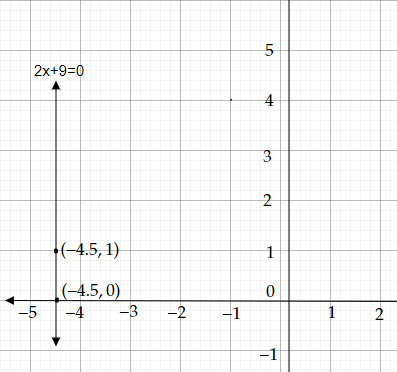
$x=-4.5$ 且 $y=0$

$2x+9=0$在單變數中的幾何表示是：

(ii) 我們知道：

要繪製雙變數線性方程的圖形，我們至少需要兩個解。

$2x+9=0$可以寫成：

雙變數形式為$2x+(0)y+9=0$。

為了找到方程$2x+(0)y+9=0$的解

讓我們在方程$2x+(0)y=-9$中代入$y=0, 1$和$x=-4.5$

我們得到：

$2(-4.5)+(0)y=-9$

$-9+0=-9$

$-9=-9$

對於$y=1$

我們得到：

$2(-4.5)+(0)1=-9$

$-9+0=-9$

$-9=-9$

因此：

$(-4.5, 0)$和$(-4.5, 1)$是方程$2x+(0)y=-9$的兩個解。

教程點

更新於：2022年10月10日

863 次瀏覽

開啟你的職業生涯

完成課程獲得認證

開始學習