模函式

---

介紹

• 一個模函式可以用來查詢數字的大小，而不管其符號如何。

• 換句話說，模函式給出數字的大小。

• 模函式還確定數字到原點的距離。

• 它始終給出函式的非負值。

• 它幾乎用於所有主要的科學測量。

• 模函式表示為as=|x|。

• 在本教程中，我們將學習有關函式、絕對（模）函式、絕對函式圖、絕對函式的性質、絕對函式定積分的規則、絕對函式的連續性和可微性、符號函式以及一些解決的示例，以幫助我們更好地理解概念。

函式

• 函式是變數和數字之間特殊型別的關係。

• 函式可以被認為是一組規則，這些規則根據給定的元素產生新的輸出。

• 考慮集合 A 和集合 B 與關係 If $\mathit{f}$，如果集合 A 的元素在集合 B 中有其像，則稱其為函式。

• 如果$\mathit{f}$是從集合 A 到集合 B 的函式，並且$\mathrm{(a,b) \in \mathit{f}, 那麼\: \mathit{f}(a) = b.}$

絕對（模）函式

• 眾所周知，模函式給出函式的絕對值，而不管其符號如何。模函式的值始終大於或等於零。它表示為f(x) = |x|，其中 f: R → (0,∞) 且 x ∈ R。

• 對於實數“x”，|x|是 x 的模。如果 x 是大於零的非零實數，則 f(x) 給出 x 的絕對值。

$$\mathrm{\begin{cases}f(x)=x & x\geq 0 \\f(x)=-x & x < 0\end{cases}}$$

絕對函式圖

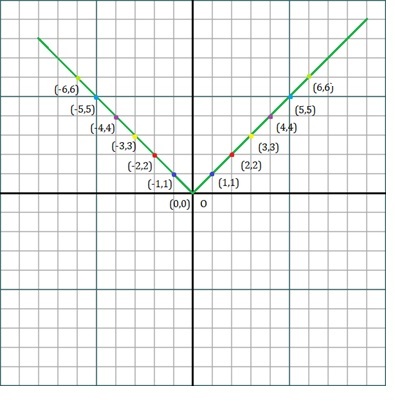
對於變數“x”，取值範圍為 -6 到 6，找到 'x' 的正值和負值的模，我們將圖形繪製為 'y = x' 和 'y = -x'。

X	-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6
f(x)=x	6	5	4	3	2	1	0	1	2	3	4	5	6

將其繪製到圖形上。

絕對函式的性質

以下是模函式的性質，可以幫助我們更好地理解其應用。

• 性質 1 - 模函式為所有實數值 x 輸出絕對值。因此，模函式始終可以為正值。

|x| = p；如果p 大於 0，則 x = ± p；

|x| = p；如果 p 等於 0，則 x = 0；

如果 |x| = p，則 x 不能為零。

• 性質 2 -

  • 情況 1：如果 p 大於 0

    |f(x)| < p 且 p > 0 ⇒ -p < f(x) < p

    |f(x)| > p 且 p > 0 ⇒ -p < f(x)（或）f(x) > p

  • 情況 2：如果 p 小於 0

    |f(x)| < p 且 p < 0；不存在任何解。

    |f(x)| > p 且 p < 0；對於所有實數值 f(x) 都是允許的。

• 性質 3 - 如果 p、q 屬於實數，則

  $$\mathrm{|-p| = |p|}$$

  $$\mathrm{|p-q| = 0 \Leftrightarrow p=q}$$

  $$\mathrm{|p+q| \leq |p| + |q|}$$

  $$\mathrm{|p-q| \geq ||p| - |q||}$$

  $$\mathrm{|pq| = |p| |q|}$$

  |p/q| = |p|/|q|，q 不等於零。

絕對函式定積分的規則

規則 1 - 為了計算模函式的定積分，我們透過將給定函式等於零來找到 x 截距。

規則 2 - 為模函式繪製的圖形的形狀始終為“V”。

規則 3 - 透過設定給定的區間，我們將積分分成幾部分並進行積分。

$$\mathrm{\begin{cases}f(x)=x & x\geq 0 \\f(x)=-x & x < 0\end{cases}}$$

模函式的積分可以寫成

$$\mathrm{\int \mathit{f}(x)=(\frac{1}{2})x^2+C \:\:\:\:\:\:\: x≥0}$$

$$\mathrm{\int \mathit{f}(x)=-(\frac{1}{2})x^2+C \:\:\:\:\:\:\: x<0}$$

絕對函式的連續性和可微性

絕對連續性允許我們獲得模函式的連續性。例如 -

對於模函式 |x+3|+|x-2|，要找到連續性，我們將它分成兩個函式 -

|x+3| 和 |x-2|

x=-3 和 x=2

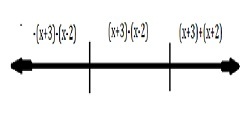
f(x)=-x-3-x+2=-2x-1 如果 x<-3

f(x)=x+3-x+2=5 如果 -3<x<2

f(x)=x+3+x-2=2x+1 如果 x≥2

現在讓我們學習絕對函式的可微性。

我們知道 f(x)=|x| 等於 x，如果 x>0，等於 -x 如果 x<0

$$\mathrm{\begin{cases}f(x)=x & x\geq 0 \\f(x)=-x & x < 0\end{cases}}$$

因此，模函式 f(x)=|x| 的導數等於 1，如果 x>0，等於 -1，如果 <0

$$\mathrm{\frac{d\{f(x)\}}{dx}=1,if\: x>0}$$

$$\mathrm{\frac{d\{f(x)\}}{dx}=-1,if\: x<0}$$

模函式的導數：$\mathrm{\frac{d\{|x|\}}{dx}=\frac{x}{\{|x|\}}}$，對於除零之外的所有 x 值。

符號函式

符號函式可以透過以下方式定義

$$\mathrm{f(x)=1,if\: x>0}$$

$$\mathrm{f(x)=0,if\: x=0}$$

$$\mathrm{f(x)=-1,if\: x <0}$$

其中 x 是實數，範圍是 {-1,0,1}

解題示例

1.求 x = -2 和 x = 5 時模函式 |x| 的值。

解答

如果 x=-2，則 |x| = |-2| =2

如果 x = 5，則 |x| = |5| = 5

答案

|x| = 2 對於 x = -2 且 |x| = 5 對於 x = 5

2.求函式 |x + 5| = 10 的模。

解答

模函式的值是非負的，出現以下情況 -

如果 x + 5> 0，則模 |x + 5| = x + 5，如果 x + 5 < 0，則 |x + 5| = -(x +5)。

情況 1 - 如果 x + 5> 0，則

|x + 5| = x + 5

⇒ x + 5 = 10

⇒ x = 10-5 = 5

情況 2 - 如果 x +5 < 0，則

⇒ -(x + 5) = 10

⇒ -x - 5 = 10

⇒ x = -5 - 10 = -15

答案：因此，解為 x = 5,-15

結論

模函式可用於查詢數字/變數的大小，而不考慮其符號。換句話說，模函式給出數字的絕對值。函式 f(x) 的模由 |x| 給出，其中 x≥0。函式可以被認為是一組規則，這些規則根據給定的元素產生新的輸出。x 的函式模，其中 x 屬於實數，由

$$\mathrm{\begin{cases}f(x)=x & x\geq 0 \\f(x)=-x & x < 0\end{cases}}$$

所有實數的集合構成模函式的定義域。

常見問題解答

1.定義符號函式的範圍。

符號函式的範圍是 {-1,0,1}

2.為什麼模函式是正數？

大於零的數字的模是正數，小於零的數字的模也是正數，而不管其符號如何。因此，模函式給出正值。

3.模函式的頂點是什麼？

對於 y=|x|，模函式的頂點是 (0,0)。

4.模函式的範圍是什麼？

一組所有大於或等於零的數字是模函式的範圍。

5.模函式的導數是什麼？

模函式在實線上不可微，但在其某些部分可微，模函式的導數為

$$\mathrm{\frac{d\{f(x)\}}{dx}=1,if\: x>0}$$

$$\mathrm{\frac{d\{f(x)\}}{dx}=-1,if\: x<0}$$