Python實現最小成本葉值樹

假設我們有一個正整數陣列arr，考慮所有滿足以下條件的二叉樹：

  • 每個節點要麼有0個子節點，要麼有2個子節點；
  • 陣列arr的值對應於樹的中序遍歷中每個葉子的值。
  • 每個非葉子節點的值等於其左右子樹中最大葉節點值的乘積。

在所有可能的二叉樹中，我們必須找到每個非葉子節點值可能的最小總和。例如，如果輸入arr為[6,2,4]，則輸出為32，因為可能有兩種樹：

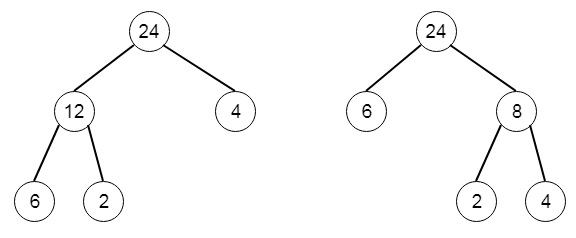
為了解決這個問題，我們將遵循以下步驟：

  • 建立一個名為memo的對映
  • 定義一個名為dp()的方法，它將i和j作為引數。它的工作原理如下：
  • 如果j <= i，則返回0
  • 如果(i, j)在memo中，則返回memo[(i, j)]
  • res := 無窮大
  • 對於k從i到j – 1的範圍
    • res := res，dp(i, k) + dp(k + 1, j) + (arr從索引i到k + 1子陣列的最大值) * (arr從k + 1到j + 1子陣列的最大值)的最小值
  • memo[(i, j)] := res
  • 返回memo[(i, j)]
  • 主方法將呼叫此dp()方法，方法如下：呼叫dp(0, arr的長度 - 1)

讓我們來看下面的實現來更好地理解：

示例

class Solution(object):
   def mctFromLeafValues(self, arr):
      """
      :type arr: List[int]
      :rtype: int
      """
      self. memo = {}
      def dp(i,j):
         if j<=i:
            return 0
         if (i,j) in self.memo:
            return self.memo[(i,j)]
         res = float('inf')
         for k in range(i,j):
            res = min(res,dp(i,k) + dp(k+1,j) + (max(arr[i:k+1])*max(arr[k+1:j+1])))
         self.memo[(i,j)]=res
         return self.memo[(i,j)]
      return dp(0,len(arr)-1)

輸入

[6,2,4]

輸出

32

更新於：2020年3月5日

382 次瀏覽

開啟你的職業生涯

完成課程獲得認證

開始學習
廣告