質量和動量

---

介紹

物體的質量是其內部物質的總量。我們知道物質是由原子和分子組成的。因此，當我們說物體的質量為“n 千克”時，這意味著物體內部所有原子和分子的單個質量總和等於“n 千克”。物體的動量和質量彼此相關，前提是物體處於運動狀態。動量是衡量運動物體所具有的能量。

什麼是質量？

物理物體內部物質的總量稱為其質量。數學上，質量可以寫成 -

$$\mathrm{m\:=\:\rho\:V}$$

其中

𝑚 表示物體的質量。

𝜌 表示物體的密度。

𝑉 表示物體的體積。

我們都知道，將一個空紙箱推過一個裝滿重物的紙箱比推空紙箱容易。從科學的角度來說，物體的質量越大，推動它所需的力就越大。因此，物體的質量也告訴我們它抵抗任何改變其當前狀態（無論是靜止狀態還是運動狀態）的能力，以抵抗施加在其上的合外力。需要注意的是，質量是一個標量量（它只有大小，沒有方向）。SI 單位是千克 (Kg)。

什麼是重量？

重量是衡量重力對任何物體施加的力的大小。數學上，重量可以寫成

$$\mathrm{W\:=\:mg}$$

這裡 𝑚 表示物體的質量，𝑔 表示重力加速度。關於重量，應注意以下幾點

• 它是一個向量量（它既有大小又有方向——朝向地球中心）。

• 其 SI 單位是牛頓

比較依據	質量	重量
定義	質量是衡量物體慣性的量度。	重量是衡量重力對物體施加的力的大小。
隨位置變化	保持不變。	它隨重力加速度的值而變化。

什麼是動量？

考慮一個質量為 m 的物體以速度 v 在直線上運動（一維運動）。然後，可以使用以下公式計算物體的線性動量

$$\mathrm{p\:=\:mv}$$

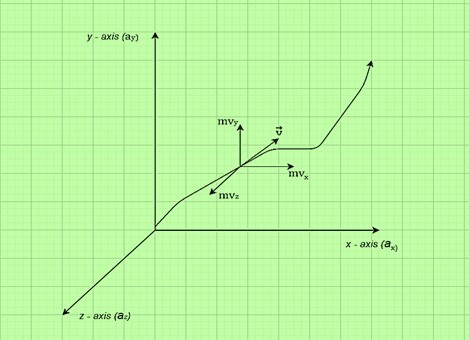
它是一個向量量。在向量形式中，它可以寫成 𝑝⃗ = 𝑚⃗𝑣⃗。如果我們根據其沿三個軸的分量表示速度，則

$$\mathrm{\overrightarrow{v}\:=\:v_{x}a_{x}\:+\:v_{y}a_{y}\:+\:v_{z}a_{z}}$$

其中 𝑎𝑥 表示沿 𝑥 − 軸的單位向量，𝑎𝑦 表示沿

𝑦 − 軸的單位向量，𝑎𝑧 表示沿 𝑧 − 軸的單位向量。

在這種情況下，物體的動量根據其沿三個軸的分量給出$\mathrm{\overrightarrow{p}\:=\:mv_{x}\:+\:mv_{y}\:+\:mv_{z}}$ 其中 𝑚𝑣𝑥、𝑚𝑣𝑦 和 𝑚𝑣𝑧 表示沿 x、y 和 z 軸動量的大小

這些分量的表示也顯示在下圖中

線性動量守恆定律

根據動量守恆定律——如果作用在一個系統上的淨外力為零，則其動量保持守恆”。

更準確地說——“在任何事件之前和之後，孤立系統的總動量保持不變”

讓我們透過一個例子來理解這一點

假設兩輛汽車 A 和 B，其質量分別為 𝑚 和 𝑀，分別以速度 𝑣1 和 𝑣2 相向行駛。一段時間後，兩輛汽車發生碰撞，其速度分別變為 𝑣3 和 𝑣4。現在，對於一個孤立的系統，根據動量守恆定律 -

$$\mathrm{碰撞前動量\:=\:碰撞後動量}$$

$$\mathrm{mv_{1}\:+\:mv_{2}\:=\:mv_{3}+\:mv_{4}}$$

但是，應注意，此定律僅適用於孤立系統——作用在其上的淨外力為 0 的系統。

動量隨物體質量的變化

我們都知道，質量為‘m’、速度為‘v’的物體的線性動量由下式給出

$$\mathrm{p\:=\:mv}$$

從上述方程式可以看出——任何運動物體的動量與其質量成正比，保持速度不變。但是，任何運動物體的動量有什麼意義呢？讓我們透過以下內容來理解這一點 -

情況 1 − 假設一輛質量為 100 千克的汽車以 50 米/秒的速度撞向一堵牆並停止。

情況 2 − 假設一輛質量為 500 千克的卡車以與汽車相同的速度 50 米/秒撞向一堵牆並停止。

現在，哪輛車——汽車或卡車，對牆造成的損壞更大？如果我們計算並比較汽車和卡車的動量，就可以很容易地回答這個問題。

對於汽車 − $$\mathrm{p_{1}\:=\:100\:\times\:50\:=\:5000kgms^{-1}}$$

對於卡車 − $$\mathrm{p_{2}\:=\:500\:\times\:50\:=\:25000kgms^{-1}}$$

很明顯，卡車的動量是汽車動量的五倍。動量也是衡量運動物體所具有的能量大小的量度。在上述情況下，卡車對牆造成的損壞是汽車對牆造成的損壞的五倍。

結論

物體的質量是其內部物質的量。如果不知道被觀測物體的質量，則數學物理學毫無用處。運動物體的動量是衡量其所具有的能量或其運動能量大小的量度。動量守恆是一個重要的定律，並用於各種現實生活場景中。

常見問題

1. 運動物體的質量是否總是保持不變？

在正常速度下，任何運動物體的質量都保持不變。但是，根據狹義相對論，當物體的速度達到光速時，物體的質量開始減小。

2. 給出一個動量守恆的現實生活例子。

槍支的後坐力。

3. 動量的變化率告訴我們什麼？

我們知道 $$\mathrm{p\:=\:mv}$$

動量的變化率將給出 $\mathrm{m\:\:\frac{dv}{dt}\:=\:ma\:=\:F}$ 因此，動量的變化率給出了作用在物體上的合外力。

4. 角動量和線性動量之間的關係是什麼？

角動量和線性動量之間的關係由下式給出 -

$$\mathrm{L\:=\:rp\sin\theta}$$

5. 你所說的質心是什麼意思？

質心是物體或物體系統中的一點，假定物體的整個質量都集中在該點。