資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法學研究低密度奇偶校驗碼 (LDPC)
低密度奇偶校驗碼 (LDPC) 是一種線性糾錯分組碼，適用於透過噪聲很大的通道傳輸的大塊資料中的糾錯。
LDPC 碼由 Robert G. Gallager 在 1960 年在麻省理工學院的博士論文中開發。因此，這些碼也稱為 Gallager 碼。
低密度奇偶校驗碼的編碼
低密度奇偶校驗 (LDPC) 碼由一個奇偶校驗矩陣指定，該矩陣主要包含 0，並且 1 的密度較低。矩陣的行表示方程，列表示碼字中的位，即碼符號。
LDPC 碼由 (n, j, k) 表示，其中 n 是塊長度，j 是每一列中 1 的數量，k 是每一行中 1 的數量，並具有以下屬性：
j 是每一列中 1 的數量的小固定數，其中 j > 3
k 是每一行中 1 的數量的小固定數，其中 k > j。
示例 1 - 漢明碼的奇偶校驗矩陣
以下奇偶校驗矩陣是具有 n = 7 的漢明碼，其中包含 4 個資訊位，後跟 3 個偶校驗位。校驗位位於對角線上。奇偶校驗方程如下所示：
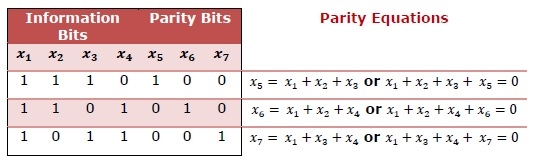
示例 2 - 低密度奇偶校驗矩陣
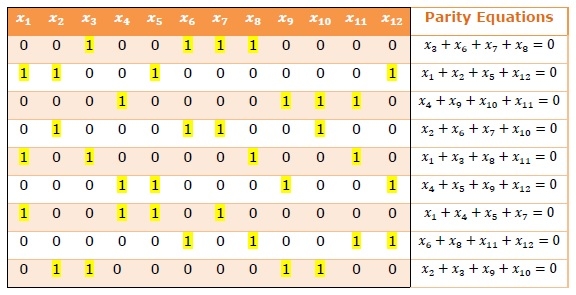
此示例說明了一個 (12, 3, 4) LDPC 矩陣，即 n = 12，j = 3，k = 4。這意味著每個方程作用於 4 個碼符號，每個碼符號出現在 3 個方程中。與漢明碼的奇偶校驗矩陣不同，此碼在校驗位中沒有任何對角線上的 1。
LDPC 碼的解碼
LDPC 碼有兩種可能的解碼技術：
在第一種技術中，解碼器根據奇偶校驗方程進行所有奇偶校驗。如果任何一位包含超過固定數量的不滿足的奇偶校驗方程，則該位的數值將被反轉。一旦獲得新值，就使用新值重新計算奇偶校驗方程。重複此過程，直到所有奇偶校驗方程都滿足為止。
這種解碼過程很簡單，但僅適用於奇偶校驗集較小的情況。
第二種方法對 LDPC 圖進行機率演算法。該圖是一個稀疏二部圖，包含兩組節點，一組表示奇偶校驗方程，另一組表示碼符號。如果方程中存在碼符號，則一條線連線第一組中的節點到第二組。
這兩種方法的兩個子類是置信傳播和最大似然解碼。雖然這些解碼演算法很複雜，但它們比前者產生更好的結果。
9K+ 瀏覽量
