資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法學如何在 Python 中執行卡方擬合優度檢驗
介紹
資料科學家經常使用統計方法進行假設檢驗，以從資料集中獲得見解。雖然有多種可用的統計方法，但這篇文章將討論卡方擬合優度檢驗及其在 Python 中的實現。卡方檢驗驗證了分類變數的觀察分佈與預期分佈是否一致。它告訴我們可用事件值是否與預期值不同。
卡方檢驗
您可以執行卡方檢驗來驗證資料集對觀察事件的分佈。卡方檢驗做了一些假設，如下所示：
變數相互獨立。
只有一個分類特徵。
每個變數都必須包含頻數超過五個的類別。
隨機抽樣的資料集。
每個資料組的頻數必須相互排斥。
卡方檢驗統計量
卡方檢驗使用以下公式給出統計輸出：
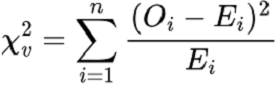
其中
v 表示自由度
O 表示樣本觀察值
E 表示總體預期值
n 表示變數類別計數。
現在讓我們學習如何執行卡方檢驗。
假設檢驗步驟
執行卡方檢驗的步驟如下：
首先，您需要建立一個零假設 H0 和一個備擇假設 H1。
然後，您需要決定接受或拒絕零假設的機率閾值。此閾值的典型值為 5%，相應的臨界值取決於分佈。
然後使用上述公式計算卡方統計量。
最後，您需要將檢驗統計量值與臨界值進行比較。如果檢驗統計量大於臨界值，則我們拒絕零假設；否則，我們不拒絕零假設。
讓我們使用上述步驟實現該檢驗：
這裡的零假設是變數以預定方式分佈。備擇假設是變數的分佈不同。我們將用下面討論的兩種方法實現卡方檢驗：
使用內建函式實現卡方檢驗
語法
chi_square_test_statistic, p_value = stats.chisquare( experience_in_years, Salary)
此函式採用兩個特徵，將卡方公式應用於它們，並返回卡方檢驗統計量和 p 值。
演算法
載入所需的依賴項，例如 scipy 和 numpy。
將要應用檢驗統計量的特徵傳遞給 scipy.stats 的卡方函式。
獲取檢驗統計量和 p 值。
根據 p 值和卡方統計量接受或拒絕零假設和備擇假設。
示例
該過程首先載入所有必要的依賴項。
# importing packages import scipy.stats as stats import numpy as np
讓我們準備一個演示資料，其中我們將有兩列“經驗年數”和“薪水”。對於此資料，我們將執行卡方檢驗。
# No of years of experience of an employee
# Yearly Salary package in lakhs
experience_in_years= [8, 6, 10, 7, 8, 11, 9]
Salary= [9, 8, 11, 8, 10, 7, 6]
# Chi-Square Goodness of Fit Test
chi_square_test_statistic, p_value = stats.chisquare(
experience_in_years, Salary)
# chi square test statistic and p value
print('chi_square_test_statistic is : ' +
str(chi_square_test_statistic))
print('p_value : ' + str(p_value))
# find Chi-Square critical value
print(stats.chi2.ppf(1-0.05, df=6))
解釋
以上程式碼是使用 Scipy 庫中的內建函式實現卡方檢驗的 Python 程式碼。從 stats 匯入的 chisquare 方法返回兩個值：卡方檢驗統計量和 p 值。此方法採用兩個特徵，將比較這兩個變數並應用上述卡方公式來計算卡方統計量。在這裡，我們比較的是經驗年數和年薪之間的關係。
輸出
chi_square_test_statistic is : 5.0127344877344875 p_value : 0.542180861413329 12.591587243743977
如我們所見，p 值為 0.54，臨界值為 12.59。檢驗統計量小於臨界值，因此我們可以接受零假設並拒絕備擇假設。
從頭開始實現卡方檢驗
語法
chi_square_test_statistic1 = chi_square_test_statistic1 + \ (np.square(experience_in_years[i]-salary[i]))/salary[i]
使用上述公式計算資料集中每個樣本的卡方值，並將它們加在一起以獲得最終分數。
演算法
載入所需的依賴項，例如 numpy。
初始化一個值為 0 的變數，該變數將儲存統計量的最終值。
迭代資料中的每個樣本，計算每個樣本的統計量，並將其新增到包含統計量最終值的變數中。
計算出統計量後，接受或拒絕零假設和備擇假設。
示例
此方法將使用公式實現卡方擬合優度檢驗。此方法將產生與上述方法相同的結果。
import scipy.stats as stats
import numpy as np
# No of years of experience of an employee
# Yearly Salary package in lakhs
experience_in_years= [8, 6, 10, 7, 8, 11, 9]
salary= [9, 8, 11, 8, 10, 7, 6]
# determining chi square goodness of fit using formula
chi_square_test_statistic1 = 0
for i in range(len(experience_in_years)):
chi_square_test_statistic1 = chi_square_test_statistic1 + \
(np.square(experience_in_years[i]-salary[i]))/salary[i]
print('chi square value determined by formula : ' +
str(chi_square_test_statistic1))
# find Chi-Square critical value
print(stats.chi2.ppf(1-0.05, df=6))
解釋
以上程式碼已在 Python 中實現，用於對相同資料執行卡方檢驗。在這種方法中，我們只在 Python 中實現了卡方統計量公式，而不是匯入內建方法。for 迴圈有助於遍歷資料集。然後，我們使用 NumPy 實現上述公式，並將分數與之前的分數相加，以獲得整個資料集的總分數。最後，我們檢查使用此方法獲得的卡方統計量。
輸出
chi square value determined by formula : 5.0127344877344875 12.591587243743977
正如我們預期的那樣，結果與我們使用先前方法獲得的結果相同。此結果還表明，我們不應拒絕零假設，但可以拒絕備擇假設。
結論
我們學習了卡方擬合優度檢驗以及如何使用 Python 實現它。讓我們用一些關鍵要點總結一下這篇文章：
卡方檢驗驗證了觀察到的分類變數的分佈與預期變數分佈是否一致。
卡方檢驗做了一些假設，包括只有一個分類變數、獨立變數、至少五個唯一類別和隨機抽樣的資料。
我們透過接受或拒絕零假設來得出檢驗結果。
為了接受零假設，閾值必須小於臨界值。
3000+ 次瀏覽
