資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究C++ 中 T 秒後青蛙的位置
假設我們有一個由 n 個頂點組成的無向樹。頂點編號從 1 到 n。現在一隻青蛙從頂點 1 開始跳躍。如果青蛙當前的頂點和另一個未訪問的頂點相鄰，它可以在一秒鐘內跳到該頂點。青蛙不能跳回已訪問的頂點。如果青蛙可以跳到多個頂點，它會隨機跳到其中一個頂點
機率相同，否則，當青蛙無法跳到任何未訪問的頂點時，它會永遠停留在同一個頂點上。
樹以邊的陣列形式給出。我們必須找到青蛙在 t 秒後位於頂點 target 的機率。
因此，如果輸入類似於 n 為 7，t 為 2，target 為 4，樹類似於 -
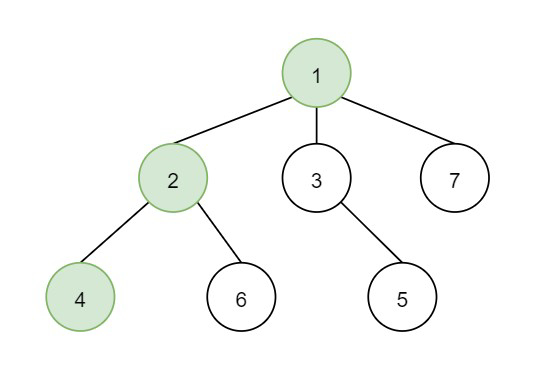
那麼輸出將為 0.1666，從圖中可以看出。青蛙從頂點 1 開始，以 0.3333 的機率在第 1 秒跳到頂點 2，然後以 0.5 的機率在第 2 秒跳到頂點 4。因此，青蛙在 2 秒後位於頂點 4 的機率為 0.3333 * 0.5 = 1.6665。
為了解決這個問題，我們將遵循以下步驟 -
ret := 1
定義一個集合 visited
定義一個函式 dfs()，它將接收節點、起點、邊列表 g、時間、t、一個棧 st，
如果節點是 visited 的成員，則 -
返回 false
將節點插入 visited
如果節點與 1 相同，則 -
tt := time，ok := true
返回 true
對於初始化 i := 0，當 i < g[node] 的大小，更新（將 i 增加 1），執行 -
將 g[node, i] 插入 st
如果 dfs(g[node, i], start, g, time + 1, t, st) 為 true，則 -
返回 true
從 st 中刪除元素
返回 false
從主方法執行以下操作 -
ret := 1
ok := false
定義一個大小為 n + 1 的列表陣列 graph
定義一個大小為 n + 1 的列表陣列 graph2
對於初始化 i := 0，當 i < edges 的大小，更新（將 i 增加 1），執行 -
將 edges[i, 1] 插入 graph[edges[i, 0]] 的末尾
將 edges[i, 0] 插入 graph[edges[i, 1]] 的末尾
定義一個棧 st
dfs(target, target, graph, 0, t, st)
當 (st 不為空) 時，執行 -
node := st 的頂部元素
sz := graph[node] 的大小
如果 node 不等於 1，則 -
(將 sz 減 1)
ret := ret * (1.0 / sz)
從 st 中刪除元素
如果 tt > t，則 -
返回 0
如果 tt 與 t 相同，則 -
返回 ret
如果 tt < t 且 target 與 1 相同且 graph[target] 的大小 >= 1，則 -
返回 0
返回（如果 tt < t 且 graph[target] 的大小 > 1，則為 0，否則為 ret）
讓我們看看以下實現以更好地理解 -
示例
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
double ret = 1;
bool ok;
set<int> visited;
int tt;
bool dfs(int node, int start, vector<int> g[], int time, int t,
stack<int>& st){
if (visited.count(node))
return false;
visited.insert(node);
if (node == 1) {
tt = time;
ok = true;
return true;
}
for (int i = 0; i < g[node].size(); i++) {
st.push(g[node][i]);
if (dfs(g[node][i], start, g, time + 1, t, st))
return true;
;
st.pop();
}
return false;
}
double frogPosition(int n, vector<vector<int> >& edges, int t,
int target){
ret = 1;
ok = false;
vector<int> graph[n + 1];
vector<int> graph2[n + 1];
for (int i = 0; i < edges.size(); i++) {
graph[edges[i][0]].push_back(edges[i][1]);
graph[edges[i][1]].push_back(edges[i][0]);
}
stack<int> st;
dfs(target, target, graph, 0, t, st);
while (!st.empty()) {
int node = st.top();
double sz = (double)graph[node].size();
if (node != 1)
sz--;
ret *= (1.0 / sz);
st.pop();
}
if (tt > t)
return 0;
if (tt == t)
return ret;
if (tt < t && target == 1 && graph[target].size() >= 1)
return 0;
return tt < t && graph[target].size() > 1 ? 0 : ret;
}
};
main(){
Solution ob;
vector<vector<int>> v = {{1,2},{1,3},{1,7},{2,4},{2,6},{3,5}};
cout << (ob.frogPosition(7,v,2,4));
}輸入
7, {{1,2},{1,3},{1,7},{2,4},{2,6},{3,5}}, 2, 4輸出
0.166667
273 次檢視
