查詢有向圖中長度為 K 的路徑數

---

給定一個有向無權圖 G 和一個整數 K。您必須找到圖中長度為 K 的路徑數。此處，圖以鄰接矩陣的形式給出。從頂點 i 到 j，如果存在邊，則表示為 G[i][j]=1，否則表示為 G[i][j]=0。

輸入

• 由鄰接矩陣表示的有向無權圖

• 表示要查詢的路徑長度的整數 K

輸出

長度為 K 的路徑總數

案例 I K=3

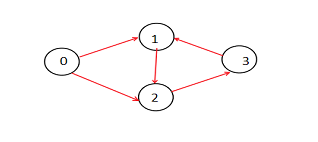
輸出

路徑總數= 2

解釋

在上圖中，有兩條長度為 3 的路徑。它們是-

• 0->1->2->3

• 0->2->3->1

案例 II K=2

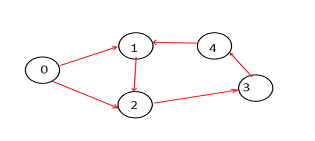
輸出

路徑總數 = 6

解釋

在上圖中，有兩條長度為 3 的路徑。它們是-

• 0->1->2

• 0->2->3

• 1->2->3

• 2->3->4

• 3->4->1

• 4->1->2

示例

import java.util.*;

public class Main {
   public static void main(String[] args) {
      int[][] G = {
         {0, 1, 1, 0},
         {0, 0, 1, 0},
         {0, 0, 0, 1},
         {0, 1, 0, 0}
      };
      int K = 3;
      List<List<Integer>> paths = fpath(G, K);
      
      System.out.println("Paths of length are");
      int count=0;
      for (List<Integer> path : paths) {
         count++;
         System.out.println(path);
      }
      System.out.println("Total number of paths "+count);
   }
   
   public static List<List<Integer>> fpath(int[][] G, int K) {
      List<List<Integer>> paths = new ArrayList<>();
      List<Integer> path = new ArrayList<>();
      boolean[] visited = new boolean[G.length];
      
      // Start the search from each vertex
      for (int i = 0; i < G.length; i++) {
         dfs(G, i, K, path, visited, paths);
      }
      
      return paths;
   }
   
   private static void dfs(int[][] G, int vertex, int K, 
List<Integer> path, boolean[] visited, 
List<List<Integer>> paths) {
      visited[vertex] = true;
      path.add(vertex);
      
      if (K == 0) {
         paths.add(new ArrayList<>(path));
      } else {
         for (int n = 0; n < G.length; n++) {
            if (G[vertex][n] == 1 && !visited[n]) {
               dfs(G, n, K - 1, path, visited, paths);
            }
         }
      }
      
      visited[vertex] = false;
      path.remove(path.size() - 1);
   }
}

輸出

Paths of length are
[0, 1, 2, 3]
[0, 2, 3, 1]
Total number of paths 2

解釋

為了找到長度等於 K 的路徑，我們將使用 DFS（深度優先搜尋）方法。有兩個輔助函式 - fpath() 和 dfs()。

fpath() 函式

• 在 fpath() 函式中，鄰接矩陣 G 和 K 作為引數傳遞。它返回一個包含列表作為路徑的列表。此外，還列印了長度為 K 的路徑總數。

• 初始化一個包含路徑的列表列表，並初始化當前路徑列表。建立一個布林陣列來標記已訪問的頂點。為每個頂點呼叫 dfs() 方法，並檢查它是否包含長度為 K 的路徑。

dfs() 函式

• dfs() 函式用於執行深度優先搜尋操作。它是一個遞迴函式。我們將傳遞圖、當前頂點、剩餘長度 K、已訪問路徑、一個跟蹤已訪問頂點的布林陣列 visited，以及“paths”（包含路徑的列表列表）來儲存路徑。

• 在給定的 dfs() 函式中，我們將標記該頂點為已訪問並將其新增到已訪問路徑中。現在訪問相鄰的頂點。如果相鄰的頂點未被訪問，則使用新頂點和剩餘長度 K-1 遞迴呼叫 dfs() 函式。

• 如果 K 的值為 0，這是我們的基本情況，則當前已訪問的路徑將新增到“paths”中。否則，如果從頂點到鄰居存在路徑並且鄰居未被訪問，則遞迴呼叫該函式。

• 訪問完所有鄰居後，將頂點標記為未訪問並將其從當前已訪問路徑列表中刪除。這也被稱為回溯。