資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究找到一個節點，使得從該節點到所有葉子節點的路徑都具有相同的顏色。
介紹
在資料結構中，一個最重要的難題是在樹中找到一個節點，其中從該節點到葉子節點的所有路徑都具有相同的顏色。本主題探討如何利用圖論和深度優先搜尋方法快速找到這些節點。透過使用顏色編碼方法並觀察其對樹遍歷的影響，這個問題可以教會我們許多關於現實世界的知識，並幫助我們提高樹相關過程的效率。
圖論基礎
圖論是計算機科學和數學中最基本的概念之一。它研究實體之間的關係，這些關係以節點和邊相連的形式表示。在這種情況下，圖是由節點（點）和邊（連線）組成的結構。這些圖可以是有向圖，其中每條邊都指向一個特定的方向，也可以是無向圖，其中連線可以雙向進行。理解路徑（由邊連線的節點序列）和葉子節點（沒有出邊的節點）對於解決現實世界中遍歷、連通性和結構問題至關重要。
理解樹和DFS的概念
樹是一種組織良好的資料結構，由透過邊連線在一起的節點組成。樹有一個根節點和從它分支出來的子節點。這形成了一個父子關係。與圖不同，樹不包含迴圈。它們在計算機科學中被廣泛用於以最佳方式組織和表示資訊。
深度優先搜尋（DFS）是一種用於遍歷圖或樹資料結構的演算法。它從一個選定的節點開始，並儘可能地沿著每個分支向下遍歷，然後再返回。它使用“後進先出”（LIFO）方法，通常使用堆疊來實現。DFS 用於查詢路徑、查詢迴圈以及分析連線元件。
樹的性質 - 樹具有關鍵性質，例如深度（從根節點到節點的距離）、高度（樹的最大深度）和度數（節點可以具有的子節點數）。除了根節點之外，每個節點都只有一個父節點，沒有子節點的節點稱為葉子節點。
性質 - 性質包括簡單性、記憶體效率以及能夠有效地找到從源節點到目標節點的路徑。
顏色編碼方案
演算法設計中的一種常見做法是使用預定義的顏色集對樹資料結構中的節點進行“著色”（或以其他方式識別）。對樹的節點進行顏色編碼可以更容易地識別趨勢和其他特徵。鑑於當前問題的性質，我們可以使用顏色編碼方案透過檢視所有通往該節點的路徑是否具有相同的顏色來縮小目標節點範圍。
在樹中為節點著色 - 在將顏色編碼方案應用於樹之前，我們定義了節點著色的標準。例如，我們可以使用不同的顏色來表示具有偶數或奇數值的節點，或者根據節點在樹中的級別使用不同的顏色。該過程涉及遍歷樹並根據所選標準為每個節點分配顏色。
理解顏色編碼方案的工作原理 - 一旦樹節點被著色，顏色編碼方案就可以讓我們快速檢查從節點到葉子節點的給定路徑是否為單色（所有節點都具有相同的顏色）。這是透過在樹遍歷和路徑探索期間進行有效的顏色比較來實現的。該方案有助於識別滿足所有通往葉子節點的路徑都具有相同顏色的條件的節點，從而輔助搜尋所需的節點。
查詢所需的節點
為了找到一個節點，使得從該節點到所有葉子節點的路徑都具有相同的顏色，我們使用一個利用顏色編碼方案的系統演算法。從根節點開始，我們遍歷樹，檢查每個節點及其對應的顏色。我們探索從節點到葉子節點的路徑，驗證這些路徑中的所有節點是否都具有相同的顏色。如果一個節點滿足此條件，我們將其標記為所需節點的潛在候選者。演算法持續進行，直到它搜尋完整棵樹或找到所需的節點。
分析時間和空間複雜度 - 演算法的效率至關重要，尤其是在大型樹的情況下。我們分析其時間複雜度，考慮諸如樹的大小和顏色編碼實現等因素。此外，我們評估空間複雜度，考慮顏色編碼樹和搜尋過程中使用的任何輔助資料結構的儲存需求。評估演算法的複雜度有助於我們瞭解其效能特徵和潛在的可擴充套件性，從而確保為當前問題提供有效的解決方案。
演算法
// Function to check if all paths from a node to leaf nodes are of the same color
function findDesiredNodeWithSameColorPaths(node):
if node is null:
return null
// Explore the subtree rooted at 'node'
resultNode = exploreSubtree(node)
// If a node with the desired property is found, return it
if resultNode is not null:
return resultNode
// Otherwise, continue searching in the left subtree
return findDesiredNodeWithSameColorPaths(node.left) OR
findDesiredNodeWithSameColorPaths(node.right)
// Function to explore the subtree rooted at 'node'
function exploreSubtree(node):
if node is null:
return null
// Check if the path from 'node' to any leaf node is of the same color
if isMonochromaticPath(node, node.color):
return node
// Continue exploring in the left and right subtrees
leftResult = exploreSubtree(node.left)
rightResult = exploreSubtree(node.right)
// Return the first non-null result (if any)
return leftResult OR rightResult
// Function to check if the path from 'node' to any leaf node is of the same color
function isMonochromaticPath(node, color):
if node is null:
return true
// If the node's color doesn't match the desired color, the path is not monochromatic
if node.color != color:
return false
// Recursively check if both left and right subtrees have monochromatic paths
return isMonochromaticPath(node.left, color) AND
isMonochromaticPath(node.right, color)
圖示
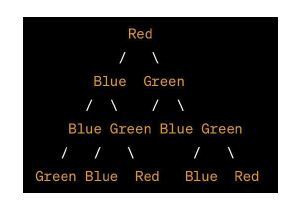
在這個二叉樹的特定圖示中，每個節點都以不同的顏色著色。紅色表示根節點，藍色表示左子節點，綠色表示右子節點。當我們向下遍歷樹時，每個左子節點的顏色從藍色變為綠色，每個右子節點的顏色從綠色變為藍色。
樹底部的葉子節點將使用綠色、藍色、綠色和紅色著色。
二叉樹通常使用顏色編碼節點來表示，以便一目瞭然地檢視其層次結構和模式。顏色編碼可以幫助快速理解樹的屬性，這在許多樹相關技術和應用中非常有用。
結論
總之，在樹中找到一個節點，其中所有通往葉子節點的路徑都具有相同顏色的問題在許多情況下都非常重要。透過使用顏色編碼和快速遍歷樹，這種方法是查詢滿足給定條件的節點的強大方法。
197 次檢視
