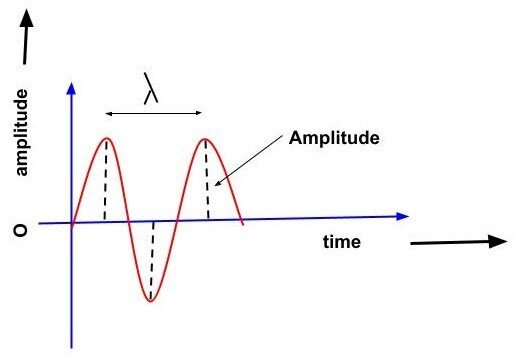
解釋波的振幅。畫出波的示意圖，並在圖上標出它的振幅。

---

介紹

波是一種從一點傳播到另一點的連續擾動。有不同型別的波透過介質傳播。主要有兩種型別的波。

機械波：需要介質才能傳播的波。例如，聲訊號在介質中傳播，水波在水中傳播。

電磁波：這些波在真空中傳播。例如，光波在太空中傳播。

通常，波以波峰和波谷的形式傳播，每個波都有一些特性，例如振幅、速度、頻率等等。在描述波時，振幅是能量的度量。對於電磁輻射，波是穿過介質或穿過空的空間的能量脈衝。

定義波的振幅

振幅是波傳遞能量的度量；投入波中的能量越多，振幅就越大，或者峰值或谷值到軸線的距離就越大，這被稱為波的振幅 (A)。

振幅以米 (m) 為單位表示。波的振幅決定了它攜帶多少能量。它估計波的起伏程度。如果波的振幅大，則能量高，而振幅小的波能量低。正弦波的方程可以寫成

$$\mathrm{x=A\:sin(\omega t+\Phi)}$$

其中：x=波的位移

A=波的振幅

ω=角頻率

t=時間

ϕ=相位角

產生粒子運動所需的能量以位移的程度表示，這被估計為波的振幅。

聲音

聲音是一種引起物體振動的能量。這些振動透過固體、液體或氣體等介質將能量從一個地方傳遞到另一個地方。由於聲音是一種縱波，因此它以壓縮和稀疏的形式傳播。當一個物體發出聲音時，物體的振動將其能量傳遞給空氣分子，引起連鎖反應，該反應透過空氣傳播，直到到達我們的耳膜。當我們的耳朵拾取到聲音時，訊號就會傳遞到我們的大腦，讓我們理解我們聽到的內容。

人類可以聽到的聲音訊率範圍為 20Hz 至 20KHz，高於和低於此範圍的聲音被稱為超聲波和次聲波。超聲波：這些波主要用於醫學領域，用於診斷各種疾病，如心電圖、超聲波檢查、體外碎石術等等。

次聲波：它是一種低頻波，最常見於火山爆發、地震等自然現象中。

在物理學中定義振幅？

振幅是由振動體或波上的一點與其靜止點之間的最大距離或位移決定的。所有波都攜帶一定的振幅。

在物理學中，波的振幅可以透過調幅來調製。在這個過程中，低振幅波在載波的幫助下將資料從源傳輸到目的地。這種調幅應用於訊號傳輸、廣播等。

聲音的特性

音調

聲音的音調是頻率的感覺。高頻聲波指的是高音調的聲音，而低頻聲波則與低音調的聲音相關。它以赫茲 (Hz) 為單位表示。

響度

波的大小決定了聲音的響度現象。如果聲波的大小很大，則表示訊號響亮。它以分貝 (dB) 為單位表示。

振幅

它是聲波穿過介質時擾動的粒子的最大位移。它以米 (m) 為單位表示。

波長

聲音是一種縱波，它透過介質傳播並經歷壓縮和稀疏。它是兩個連續的稀疏或壓縮的核心之間的空間，或者壓縮長度加上相鄰稀疏的長度。它以埃 (Å) 為單位表示，等於 10^-10 米。

$$\mathrm{\lambda=\frac{
u}{f}}$$

頻率

每秒產生的聲波數量稱為頻率。如果一個波的頻率低，則它的波比高頻波少。聲音的頻率以赫茲 (Hz) 估計。

$$\mathrm{f=\frac{1}{T}}$$

週期

介質粒子完成一次振動所需的時間稱為波的週期。它以秒(秒) 為單位表示。

$$\mathrm{T=\frac{1}{f}}$$

速度

聲波的速度是擾動從一個粒子傳播到下一個粒子的速率。它以 (ms^-1) 為單位表示。

$$\mathrm{速度=位移/時間}$$

結論

在我們的日常生活中，我們會遇到各種各樣的波，例如太陽波、水波和聲波。波只是能量以擾動形式的傳遞。

聲波是由振動物體產生的，它將能量傳遞給大氣中存在的分子。因此，聲波得以傳播。聲音有很多種，例如悅耳的聲音、噪音、音樂等等。聲音的特性在音樂或任何其他型別的聲音的產生中起著重要的作用。

常見問題

Q1. 寫出音調和響度之間的區別？

答：

音調	響度
聲音的音調是頻率的感覺。高頻聲波指的是高音調的聲音，而低頻聲波則與低音調的聲音相關。	聲波的振幅決定了聲音的響度現象。如果聲波的振幅大，則聲音響亮。
音調的SI單位是赫茲(Hz)。	響度的SI單位是分貝 (dB)。
音調與頻率成正比。	響度與振幅的平方成正比。

表1：音調和響度之間的區別

Q2. 區分音調和頻率？

答：頻率指的是事件發生的頻率。為簡單起見，我們將頻率定義為每秒發生的次數。音調是一個與頻率密切相關的術語。聲音振盪的頻率與其音調成正比。頻率的特性在所有型別的波中都有體現，包括電磁波和機械波。音調是一個專門針對聲波的特性。音調是一個難以定義的概念。

Q3. 人耳的聽力範圍是多少？

答：人可以感知20 Hz至20 kHz頻率範圍內的聲波。(有趣的是，新生兒可以聽到略高於20 kHz的頻率，但隨著年齡的增長，他們會失去一些高頻靈敏度。)

Q4. 寫出顯示波長、頻率和速度之間相關性的方程式？

答：波長、頻率和速度之間的關係可以用以下方程式表示。

$$\mathrm{\lambda=
u/f}$$

正如我們在公式中看到的；波長和速度成正比，而波長和頻率成反比。速度和頻率成正比。

Q5. 寫出三種不同格式的波長方程式。

答：求波長

$$\mathrm{λ=
u/f}$$

求頻率

$$\mathrm{f=
u/\lambda}$$

求速度

$$\mathrm{
u=f×\lambda}$$