電子自旋

---

簡介

我們知道原子的結構與太陽系相同。在太陽系中，太陽是中心，其他行星沿著特定的軌道圍繞它旋轉，就像原子核位於中心，電子圍繞它旋轉一樣。然而，我們發現行星也在其固定位置自轉。這一發現導致了電子在固定位置的自旋和旋轉。這就是為什麼科學家開始研究並發現電子也旋轉。1925年，兩位科學家 Goutsmit 和 Ulhenbeck 推匯出電子也具有角動量的想法，稱為自旋。

什麼是電子自旋？

根據 1920 年的一項實驗，電子具有兩種型別的運動；一種是圍繞原子核，另一種是圍繞固定軸。電子圍繞原子核旋轉，但在軸線上，它們旋轉和自旋。因此，第四個量子數是電子自旋量子數，它表示電子圍繞固定軸的旋轉。這種電子自旋是電子的量子屬性，其表示法為 ms。此屬性是基本量，具有固定的大小。自旋分為兩種型別；自旋向上，表示為 $\mathrm{+\frac{1}{2}}$，自旋向下，表示為 $\mathrm{-\frac{1}{2}}$。電子自旋的公式為 $\mathrm{S=\sqrt{s(s+1)h}}$。這裡，s 是量子化的自旋向量，h 是普朗克常數。

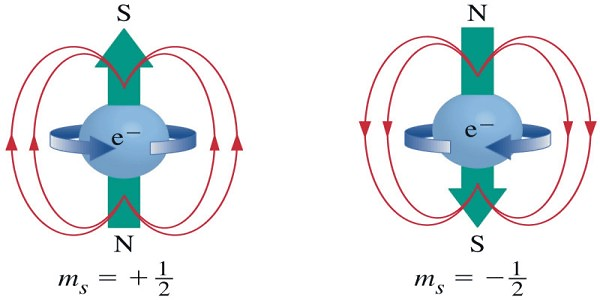
圖：1 電子的自旋

Ashurov sindor，Elektronlar-spinlarining-yo'nalishlari，CC BY-SA 4.0

眾所周知，運動的電荷是磁場的來源。因此，當電子旋轉或自旋時，它會在自身周圍產生磁場。當它順時針旋轉時，稱為自旋向上，上側為南極，下側為北極，而在逆時針方向上，它為自旋向下，極性與自旋向上相反。

電子自旋理論

電子自旋理論表明，電子與行星和球體不同，而是一個量子粒子。此外，該理論提供了有關磁場方向和自旋的資訊，並解釋了電子自旋的極性。藉助該理論，我們可以計算和假設原子的磁性。

自旋量子數

自旋量子數可以表示為電子的角動量。當電子在其軸上自旋時，它會關聯兩種型別的動量；角動量和軌道角動量。眾所周知，角動量既有方向又有大小，因此它是向量量。電子軌道有兩個位置可以容納兩個自旋；一個是自旋向上，一個是自旋向下。因此，在兩個分子之間形成鍵合時，電子優先填充軌道，然後再開始配對。自旋量子數的符號為 ms。

電子的自旋磁矩

自旋磁矩是由於電子的自旋而產生的磁矩。按照慣例，我們可以說自旋磁矩與自旋角動量有一定的關係。因此，我們可以藉助狄拉克方程推匯出自旋和磁矩之間的關係。使用狄拉克方程，我們得到

$$\mathrm{\mu _{s}=2\gamma S}$$

從上述關係中，我們發現由於自旋引起的磁矩是經典方法預期值的 2 倍。因此，我們需要磁矩，可以透過分析運動電子上的有效磁場來確定。在此之後，我們得到，

$$\mathrm{\mu _{s}=g\gamma S}$$

這裡，g 稱為 g 因子，其值為 2.002319

我們可以注意到實驗值或觀察值與預期值之間存在差異。該差異可以透過量子電動力學來定義，該理論指出帶電粒子可以與電磁場一起工作。

因此，電子的自旋磁矩

$$\mathrm{\mu _{s}=-g\frac{e}{2m}S}$$

這裡，我們知道 S 是自旋磁矩，其值為 $\mathrm{\sqrt{s(s+1)h}}$。使用 S 的值，我們得到

$$\mathrm{\left|\mu _{s} \right|=-g\mu _{B}\sqrt{s(s+1)}}$$

$$\mathrm{\left|\mu _{s} \right|\simeq \sqrt{3\mu _{B}}}$$

因此，上述方程指出電子的自旋磁矩是玻爾磁子的 $\mathrm{\sqrt{3}}$ 倍。

電子自旋理論的結果

電子自旋理論指出，電子不是完全球形的，而是一個量子粒子。電子自旋理論的一些重要結果。

• 我們可以知道原子的磁性

• 它還有助於我們找到自旋和磁場的方向

• 我們還可以分析兩個軌道的鍵合機制和磁對鍵合的影響。

解答問題

Q1。$\mathrm{Fe^{2+}}$的自旋磁矩是多少？

解：我們知道 $\mathrm{Fe^{2+}}$的自旋磁矩。其構型為 $\mathrm{1s^{2}2s^{2}2p^{6}3s^{2}3p^{6}3d^{6}}$。有 4 個未配對電子。因此，磁矩

$$\mathrm{\mu _{B}=\sqrt{n(n+2)}}$$

我們知道 n=4

$$\mathrm{\mu _{B}=\sqrt{4(4+2)}}$$

$$\mathrm{\mu _{B}=\sqrt{4\times 6}}$$

$$\mathrm{\mu _{B}\approx 5\:BM}$$

現在，自旋磁矩 $\mathrm{\left|\mu _{s} \right|\simeq \sqrt{3}\times 5}$

常見問題

Q1。什麼是角動量的量子化？

答：角動量的量子化指出，如果我們取角動量的值為軌道量子動量，則其值為 $\mathrm{L=\sqrt{l(l+1)h}}$的形式。

Q2。什麼是量子數？

答：量子數是一組四個數字，用於確定電子的各種資訊，如位置、形狀、能量、方向等。

Q3。什麼是方位量子數？

答：方位量子數是角動量量子數的第二個名稱，它顯示了軌道角動量的值。用 l 表示。

Q4。什麼是玻爾磁子？

答：當電子以 h 的軌道角動量執行時，其磁偶極矩的值稱為玻爾磁子。

Q5。玻爾磁子的值是多少？

答：玻爾磁子的值為 $\mathrm{9.27\times 10^{-24}焦耳/特斯拉}$。