回溯法和分支限界法的區別

---

回溯法是一種用於解決決策問題的演算法，而分支限界法是一種用於解決最佳化問題的演算法。這兩種技術都遵循蠻力法，並用於生成狀態空間樹。狀態空間樹是表示問題所有可能狀態的樹，從根節點到終端節點。

讓我們逐一學習這兩種技術，並詳細瞭解它們的區別。

回溯法

回溯法是對蠻力法的改進過程，該技術有效地搜尋所有可用選項中的問題解決方案。

蠻力法只不過是找到所有可能的解決方案來滿足給定問題。

蠻力法的例子：

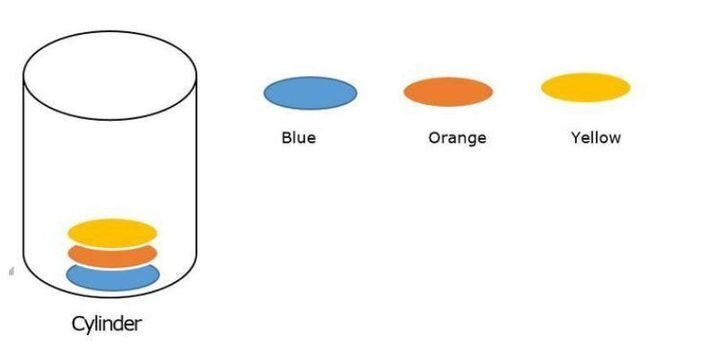
在下圖中，有三種顏色需要使用蠻力法的所有可能解決方案填充到圓柱體中。

以下是用顏色填充圓柱體的方法：

• 藍色、橙色、黃色

• 藍色、黃色、橙色

• 橙色、藍色、黃色

• 橙色、黃色、藍色

• 黃色、藍色、橙色

• 黃色、橙色、藍色

共有6種方法可以將顏色填充到圓柱體中，這就是我們可以在回溯法中修改解決方案的方法。

與回溯法相關的以下要點：

• 回溯解決方案可以用樹的形式表示，也稱為狀態空間樹。

• 回溯法遵循深度優先搜尋 (DFS)。

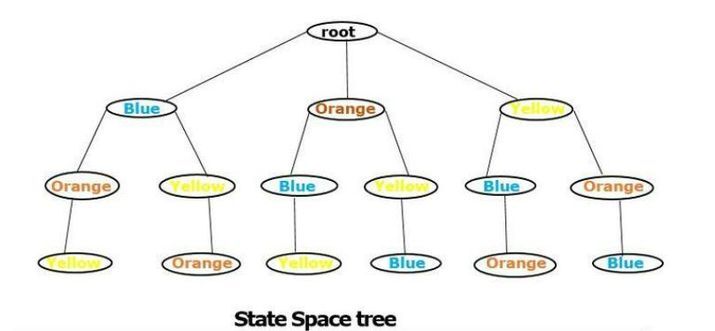
在下圖中，我們使用回溯法進行了樹形解決方案。

• 根據約束條件，我們根據約束條件解決問題。例如，我們刪除每個節點末尾的橙色，這顯示了問題時間複雜度的降低。

• 它涉及一個可行性問題。

分支限界法

分支限界法是一種用於解決最佳化問題的演算法，它透過將問題分解成更小的子問題，並透過邊界函式消除不包含最優解的子問題來解決。

分支限界搜尋是一種將深度優先搜尋的節省空間的方法與啟發式資訊相結合的方法。分支限界搜尋的思想是保持最低成本路徑或最小路徑。

此技術包含兩部分：

• 分支 - 找到多個選擇

• 限界 - 設定解決方案質量的界限。

分支限界法遵循廣度優先搜尋 (BFS)。

現在我們使用 BFS 查詢 R 到 G 的路線並建立樹。

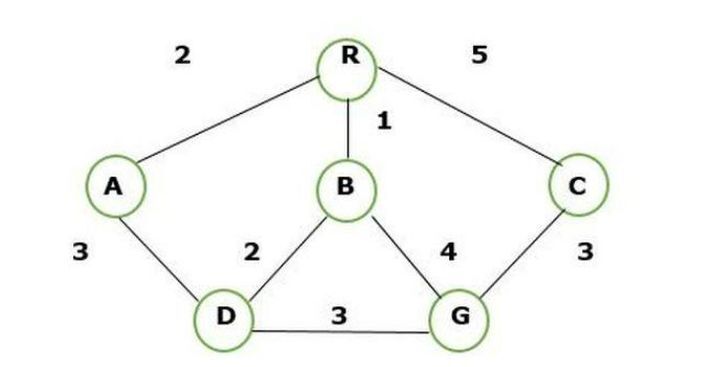
下面給出解決 BFS 方法的步驟：

步驟 1 - 我們知道源節點或根節點是 R。

步驟 2 - 訪問根節點的後繼節點，即 A、B 和 C。

步驟 3 - 將 A 的路徑節點擴充套件到 D，B 擴充套件到 D 和 B 擴充套件到 G，以及 C 擴充套件到 G。

步驟 4 - 現在完整的結構變為

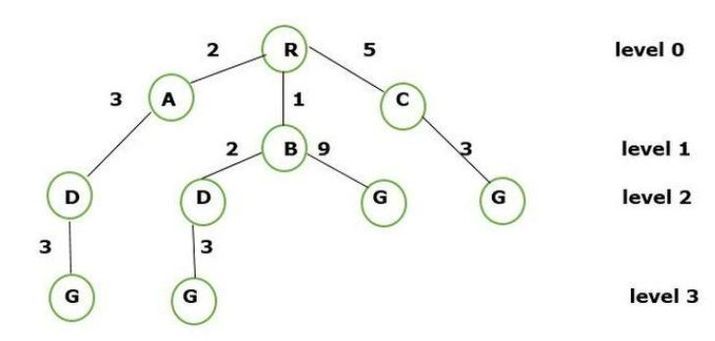
樹結構節點的層次空間劃分：

層級 0 - R

層級 1 - R -> A，R -> B，R -> C

層級 2 - R -> A -> D，R -> B -> D 和 R -> B -> G，R -> C -> G

層級 3 - 最後，連線路徑和節點權重的計算如下所示

R -> A -> D -> G (3+3+2 = 8)，R -> B -> D -> G (3+2+1 = 6) 和 R -> B -> G (9+1 = 10)，R -> C -> G (5+3 = 8)

我們從節點 R 到 G 的最短路徑是

R -> B -> D -> G = (3+2+1) = 6

就這樣我們解決了廣度優先搜尋的方法。

與分支限界法相關的以下要點：

• 此技術可以以任何方式遍歷 DFS 或 BFS。

• 它涉及一個邊界函式。

• 它透過針對最優解來完全搜尋狀態空間樹。

回溯法與分支限界法的區別

引數	回溯法	分支限界法
用途	用於解決基於決策的問題。	用於解決最佳化問題。
節點	這是一個狀態空間樹，其中節點探索深度優先搜尋。	這探索了最佳化問題。
效率	更高效。	效率較低。
函式	它涉及可行性函式。	它涉及邊界函式。
遍歷	它透過深度優先搜尋遍歷樹	它透過廣度優先搜尋遍歷樹
解決的問題	回溯法可以解決國際象棋和數獨遊戲。	它不解決任何遊戲問題。
應用	此應用程式用於解決 N 皇后問題、哈密頓迴圈和基於圖著色的問題。	此類應用程式用於解決基於旅行商問題的難題。

結論

我們看到了兩種演算法之間的區別，更好的方法是分支限界法，它遵循 BFS 搜尋。其次，分支限界法的最佳之處在於它針對最優解，而回溯法中的目標節點基於決策問題。在解決這些問題陳述時，BFS 比 DFS 需要更多的記憶體。