資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究A*演算法和AO*演算法的區別
在人工智慧和計算機科學領域，搜尋演算法對於解決具有挑戰性的問題至關重要。想象一下，你在一個巨大的迷宮中尋找出口。你可能會無目的地嘗試每條路徑，希望最終能找到出口。但是，如果有一個熟悉迷宮的嚮導來幫助你，豈不是更好？在數字領域，搜尋演算法就像迷宮中的嚮導！它們幫助計算機像你在迷宮中一樣，在眾多選項中確定最佳路徑。A* 和 AO* 就是兩個這樣的演算法。在這篇博文中，我們將討論它們的定義、機制以及它們之間的主要區別。
引言
計算機使用專門的演算法來找到複雜問題的有效解決方案，例如選擇穿過迷宮的最佳路徑或在遊戲中做出決策。A*（發音為“A-star”）和 AO*（發音為“A-O-star”）是這兩種演算法的示例。它們都希望找到到達目標的最快路徑，但它們採取不同的方法，並且關注不同的問題。
什麼是演算法？
在我們繼續討論 A* 和 AO* 之前，讓我們先構建一個演算法。計算機使用一組稱為演算法的指令來執行任務或解決問題。例如，你用來烘焙蛋糕的食譜就是一個演算法。在這個例子中，為了獲得期望的結果——一個美味的蛋糕——它指導你完成過程的每一步！
什麼是搜尋演算法？
搜尋演算法就像解決問題的超級英雄。當主要目標是確定最佳選擇並且有多個選項時，它們就會發揮作用。想象一個電腦遊戲，你的角色需要到達一個寶箱。可能存在無數條路徑，但有些路徑可能很清晰，而另一些路徑可能包含怪物。為了到達寶箱，搜尋演算法會評估每條路徑，並選擇最短和最安全的路徑！
關鍵術語
- 尋路：找到從一點到另一點的最佳路徑。
- 圖遍歷：圖遍歷是指訪問圖中的每個節點/點，圖是由連線的點組成的網路。
- 啟發式：一種智慧猜測，用於估計從任何給定節點到達目標的成本。
什麼是 A* 演算法？
A* 的功能類似於一個非常聰明的尋路者。想象一下，你在迷宮中試圖找出最快逃脫的路徑。藉助 A* 演算法，你可以找到這條路徑，它會考慮你已經走過的距離以及剩餘的距離。它將這兩個因素結合起來，在每個階段確定最佳選擇，確保快速有效地完成你的任務。A* 透過將這些成本 (f) 相加來確定最佳行動方案。
f(n) = g(n) + h(n)
- g(n)：從起點到當前節點的實際成本。
- h(n)：從當前節點到目標的估計成本。
A* 如何工作？
A* 使用兩條主要資訊
- G 值：這是從起點到當前點所花費的成本。
- H 值（啟發式）：H 值（啟發式）提供從當前位置移動到目標的成本估計。
A* 演算法示例
假設你在迷宮中
- G 值是你已經走過的步數。
- H 值是你認為還需要走多少步。
A* 將透過始終選擇 G + H 最小的路徑來幫助你找到最短路徑。
| 步驟 | 已走路徑（G 值） | 估計剩餘路徑（H 值） | 總成本（F 值） |
| 1 | 2 步 | 6 步 | 8 |
| 2 | 3 步 | 4 步 | 7 |
| 3 | 4 步 | 2 步 | 6 |
什麼是 AO* 演算法？
AO* 演算法是另一種解決問題的技術，儘管它僅限於需要決策並將問題分解成可管理部分的任務。AO* 演算法是為動態情況設計的 A* 演算法的變體。它不必重新開始搜尋以適應變化。想象一個機器人穿過一個區域，傢俱不斷移動。假設你必須在解決謎題時在每個轉彎處做出決定。藉助 AO* 演算法，你可以透過確定最佳行動方案組合來更快地解決謎題。
AO* 如何工作？
AO* 稍微複雜一些，因為它處理所謂的 AND-OR 圖。這意味著，除了只考慮一種可能的路徑（如 A*）之外，該演算法還會考慮可能協同解決問題的多種選擇。
- AND 節點：這些是必須同時做出多個選擇才能繼續的點。
- OR 節點：這些是必須從多個選項中選擇一個才能繼續的點。
AO* 演算法將這些選擇組合起來以找到問題的最佳解決方案。
AO* 演算法示例
可以這樣理解
- AND 節點：如果你想烤蛋糕，你需要麵粉 AND 糖。
- OR 節點：香草 OR 巧克力是你的蛋糕調味料選擇。
AO* 將檢查這些組合中的每一個，以檢視哪個食譜能做出最美味的蛋糕。
A* 和 AO* 演算法之間的主要區別
現在我們已經熟悉了 A* 和 AO* 演算法的基本知識，讓我們在一個簡單的表格中檢查它們之間的主要區別
| 特徵 | A* 演算法 | AO* 演算法 |
| 問題型別 | 尋路（找到最短路徑） | 決策（找到最佳策略） |
| 圖型別 | 簡單圖 | AND-OR 圖 |
| 決策 | 一次考慮一條路徑 | 考慮多條路徑和組合 |
| 複雜度 | 不太複雜 | 更復雜 |
| 用例 | 迷宮求解、GPS 導航 | 遊戲策略、複雜問題解決 |
使用 Python 程式碼和視覺化進行實現
A*（A 星）演算法是一種流行的尋路和圖遍歷演算法，用於查詢從起始節點到目標節點的最短路徑。它結合了 Dijkstra 演算法和貪婪最佳優先搜尋的優點。使用 Python 程式碼和視覺化來實現 A* 演算法
import matplotlib.pyplot as plt
import numpy as np
import heapq
# Define the grid and obstacles
grid_size = (10, 10)
start = (0, 0)
goal = (9, 9)
obstacles = [(4, i) for i in range(4, 7)] + [(i, 4) for i in range(4, 7)]
def heuristic(a, b):
return abs(a[0] - b[0]) + abs(a[1] - b[1])
def a_star(grid_size, start, goal, obstacles):
open_set = []
heapq.heappush(open_set, (0 + heuristic(start, goal), 0, start))
came_from = {}
g_score = {start: 0}
f_score = {start: heuristic(start, goal)}
while open_set:
_, current_g, current = heapq.heappop(open_set)
if current == goal:
path = []
while current in came_from:
path.append(current)
current = came_from[current]
path.append(start)
path.reverse()
return path
for dx, dy in [(-1, 0), (1, 0), (0, -1), (0, 1)]:
neighbor = (current[0] + dx, current[1] + dy)
if (0 <= neighbor[0] < grid_size[0] and
0 <= neighbor[1] < grid_size[1] and
neighbor not in obstacles):
tentative_g_score = g_score[current] + 1
if neighbor not in g_score or tentative_g_score < g_score[neighbor]:
came_from[neighbor] = current
g_score[neighbor] = tentative_g_score
f_score[neighbor] = tentative_g_score + heuristic(neighbor, goal)
heapq.heappush(open_set, (f_score[neighbor], tentative_g_score, neighbor))
return []
def plot_path(grid_size, obstacles, path):
grid = np.zeros(grid_size)
for (i, j) in obstacles:
grid[i, j] = -1
for (i, j) in path:
grid[i, j] = 1
plt.imshow(grid, cmap='Greys', interpolation='none')
plt.colorbar()
plt.title("A* Pathfinding")
plt.show()
path = a_star(grid_size, start, goal, obstacles)
plot_path(grid_size, obstacles, path)
輸出
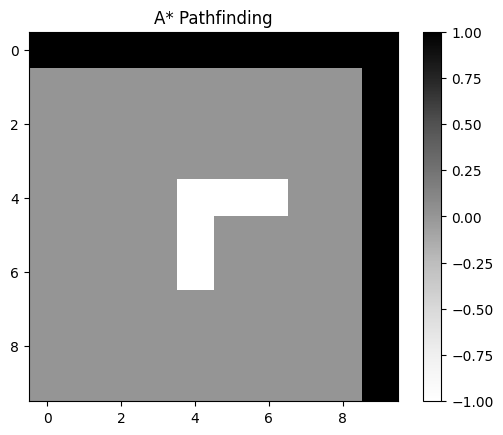
AO* 演算法
AO*（And-Or）演算法用於決策涉及多個子目標的問題。它通常用於涉及複雜問題解決的場景，其中一個動作可能導致多個結果。以下是一個帶有視覺化的簡單示例
import networkx as nx
import matplotlib.pyplot as plt
def create_ao_graph():
G = nx.DiGraph()
G.add_edges_from([('Start', 'A'), ('Start', 'B'),
('A', 'C'), ('A', 'D'),
('B', 'D'), ('B', 'E'),
('C', 'Goal'), ('D', 'Goal'), ('E', 'Goal')])
return G
def plot_ao_graph(G):
pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=True, node_size=2000, node_color='lightblue',
font_size=10, font_weight='bold', arrows=True)
plt.title("AO* Search Graph")
plt.show()
def ao_star_search(graph, start, goal):
# Simplified AO* search algorithm (pseudo-implementation)
path = []
nodes = nx.dfs_preorder_nodes(graph, source=start)
for node in nodes:
if node == goal:
path.append(node)
break
path.append(node)
return path
G = create_ao_graph()
plot_ao_graph(G)
path = ao_star_search(G, 'Start', 'Goal')
print("AO* Path:", path)
輸出
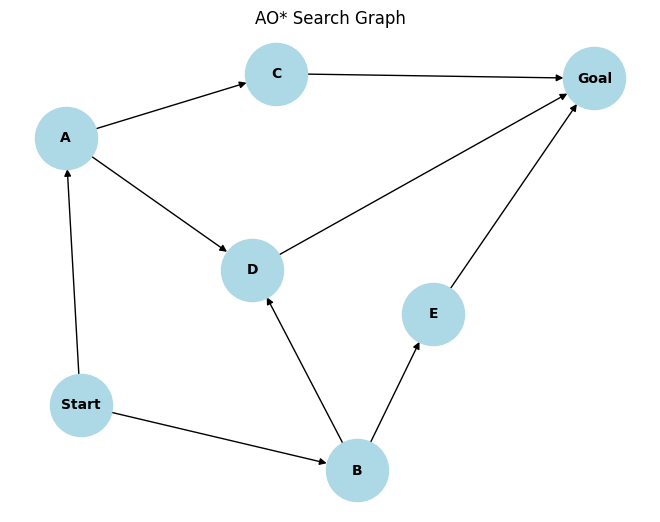
關於 A* 與 AO* 演算法的常見問題
問：還有其他搜尋演算法嗎？
答：當然！存在許多搜尋演算法，每種演算法都有其獨特的優勢和劣勢。深度優先搜尋和廣度優先搜尋是兩個流行的例子。
問：AO 能處理即時變化嗎？
答：是的，AO* 被設計為能夠有效地處理即時變化。
問：什麼是啟發式？
答：啟發式類似於一種知情的估計。在 A* 演算法中使用啟發式來估計到目標的距離。它們透過將演算法引導到正確的方向來提高其速度和效率。
結論
瞭解 A* 和 AO* 演算法之間的區別可以幫助你更好地理解計算機如何解決一般問題，例如在遊戲中確定最佳行動方案或在地圖上找到最短路徑。A* 專注於尋路，而 AO* 透過考慮不同的行動組合來解決決策問題。兩者都是計算機科學領域中有效的工具，各自具有獨特的優勢。透過理解這些演算法，你可以更好地理解計算機科學和人工智慧中尋路和圖遍歷的複雜性。
1K+ 次瀏覽
