資料處理與資料表示

---

介紹

資料處理和資料表示是系統地收集和呈現資料的過程。資料處理是指收集一組資料並將其以各種格式呈現的行為。收集、維護和呈現資料以促進分析、預測和決策的行為被稱為資料處理。在本教程中，我們將簡要討論資料處理、集中趨勢、頻數表、如何在圖表中表示資料以及與資料處理相關的示例。

什麼是資料處理？

最初收集的觀察結果稱為原始資料。任何型別的資料都可以接受。可以包括文字、統計資料、測量值、描述或觀察結果。資料管理是指確保在分析過程完成期間和之後安全可靠地收集、儲存或處置研究資料的過程。

什麼是集中趨勢？

集中趨勢的統計度量被定義為整個分佈或資料集的單個值。它旨在對分佈中的所有資料進行精確的描述。一般來說，可以使用幾種統計度量來確定資料集的集中趨勢。集中趨勢有三種度量：

• 平均數 − 資料集的平均值由平均數表示。可以透過將資料集中的所有值的總和除以值的總數來確定。

• 中位數 − 資料集的中位數（無論它是按升序還是降序排列）是其中間值。當資料集中的專案數量為偶數時，可以透過對中間兩個值取平均值來計算中位數。

• 眾數 − 資料集中出現頻率最高的值由眾數表示。資料集有時可能有一個或多個眾數，或者根本不包含任何眾數。

什麼是頻數分佈表？

在統計學中，頻數分佈表是對定量變數原始資料的排列的完整表示。該表顯示變數的不同值的頻數分佈。頻數分佈有兩種型別：離散型和連續型。可以使用計數標記為離散和連續資料值構建頻數分佈表。

資料的圖形表示

數值資料的分析可以透過圖形表示來完成。它使用圖形來顯示資料、想法、資訊和概念之間的關係。特定區域中的資訊型別始終是一個因素。線圖、條形圖、直方圖、餅圖和其他圖形表示是各種型別的示例。

已解決示例

1) 求給定資料 23, 21, 18, 16, 15, 13, 12, 10, 9, 7, 6, 5, 2 的平均數。

答案 − 平均數 = 所有觀測值的總和 / 觀測值的總數 = (23 + 21 + 18 + 16 + 15 + 13 + 12 + 10 + 9 + 7 + 6 + 5 + 2) / 13 = 157 / 13 = 12.076

2) 求給定資料 34, 56, 5, 8, 19, 67, 23, 47, 11, 86 的中位數。

答案 − 總觀測值是 10，為偶數，因此在按升序或降序排列後，我們需要計算中間兩個數字的平均值。

按升序排列的資料是 5, 8, 11, 19, 23, 34, 47, 56, 67, 86。

中位數 = (23 + 34) / 2 = 28.5

3) 求給定資料 3, 5, 5, 8, 18, 6, 2, 7, 7, 8, 6, 7 的眾數。

答案 − 眾數是重複次數最多的資料，從以上資料中，5、6和8重複兩次，7重複三次。因此，給定資料的眾數是 7。

4) 為給定的 50 個值的數集構建類間距為 10 的頻數分佈。

111, 167, 124, 105, 138, 141, 154, 162, 125, 151, 122, 184, 171, 165, 158, 174, 156, 172, 160, 143, 132, 109, 113, 155, 162, 115, 116, 168, 105, 164, 154, 182, 147, 146, 198, 162, 160, 106, 193, 186, 191, 191, 112, 167, 178, 159, 158, 153, 144, 107

答案 − 給定類間距為 10，

100-110, 110-120，依此類推，直到 190-200

類間距	頻數
100-110	5
110-120	4
120-130	3
130-140	2
140-150	5
150-160	10
160-170	11
170-180	4
180-190	3
190-200	3
總頻數	50

5) 使用在示例 4 中構建的頻數分佈表計算給定資料集的平均數。

答案 − 要找到平均數，首先，我們需要找到類間距的中點，然後我們需要找到中點和頻數的乘積。

類間距	頻數 (f)	中點 (M)	f.M
100-110	5	105	525
110-120	4	115	460
120-130	3	125	375
130-140	2	135	270
140-150	5	145	725
150-160	10	155	1550
160-170	11	165	1815
170-180	4	175	700
180-190	3	185	555
190-200	3	195	585
總頻數	50		總計 = 7560

現在平均數是 μ = Σ f.M / Σ f = 7560 / 50 = 151.2

6) 求以下資料的平均數

答案 − 要找到平均數，首先我們需要找到類間距的中點，然後我們需要找到中點和頻數的乘積。

類間距	10-20	20-30	30-40	40-50	50-60	60-70	70-80	80-90	90-100
頻數	4	6	8	10	12	14	7	5	6

類間距	頻數 (f)	中點 (M)	f.M
10-20	4	15	60
20-30	6	25	125
30-40	8	35	280
40-50	10	45	450
50-60	12	55	660
60-70	14	65	550
70-80	7	75	525
80-90	5	85	425
90-100	6	95	570
總頻數	72		總計 = 3645

現在平均數是 μ = Σ f.M / Σ f = 3645 / 72 = 50.625

7) 餅圖被分成五個部分，每個部分的角度分別為 4x、7x、6x、3x 和 10x。確定 x 的度數值。

答案 − 餅圖中所有角度的總和為 360°

4x + 7x + 6x + 3x + 10x = 360°

30x = 360° ⇒ x = 12°

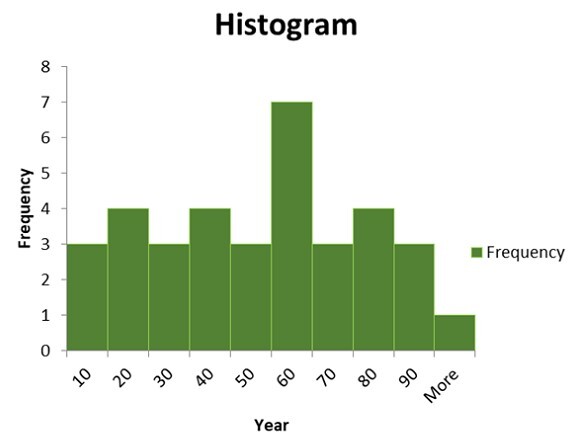
8) 繪製以下給定年齡資料的直方圖。

54,57,23,12,7,45,36,78,29,91,9,45,33,37,47,59,62,89,76,56,87,29,11,18,19,81,76, 75,56, 51,39,9,61,54,63

答案 −

現在可以使用頻數直方圖顯示此資料。

結論

資料管理是收集一組資料並將其以多種格式呈現的過程。“資料處理”是統計學中一個重要的概念，它確保研究資料的完整性，因為它處理多個關鍵方面，包括安全性、機密性和研究資料的儲存。

常見問題

1. 與其他資料表示方法相比，圖表有哪些優勢？

使用圖表的一些好處如下：

• 任何人都可以在沒有任何預備知識的情況下理解圖表。

• 它節省時間，使我們能夠關聯和對比來自不同時間段的事實。

• 它用於統計學，用於計算各種資料集的平均數、中位數和眾數，以及用於資料插值和外推。

2. 資料處理涉及哪些步驟？

資料處理過程的步驟如下：

• 問題識別

• 資料收集

• 資料呈現

• 圖形表示

• 資料分析

• 結論

3. 如何使用頻數分佈表？

頻數分佈表有助於對提供的資料進行計算。需要進行包括集中趨勢、方差、統計檢驗和分析在內的計算。此外，頻數分佈表有助於以整潔且易於理解的方式呈現資料。

4. 存在哪些不同形式的頻數分佈？

以下是一些頻數分佈：

• 分組頻數分佈。

• 非分組頻數分佈。

• 累積頻數分佈。

• 相對頻數分佈。

• 相對累積頻數分佈